机器学习(持续学习更新)
课程链接:
https://www.bilibili.com/video/BV1Bq421A74G/?spm_id_from=333.337.search-card.all.click
1.机器学习概述
1.1.监督学习
1.监督学习:input -> output,给定输入x 映射到 输出y。
给输入x的正确标签y以供学习。
通过输入x和所需输出标签y的正确对,学习算法最终学会只接受输入而无需输出标签并给出合理预测。
例如: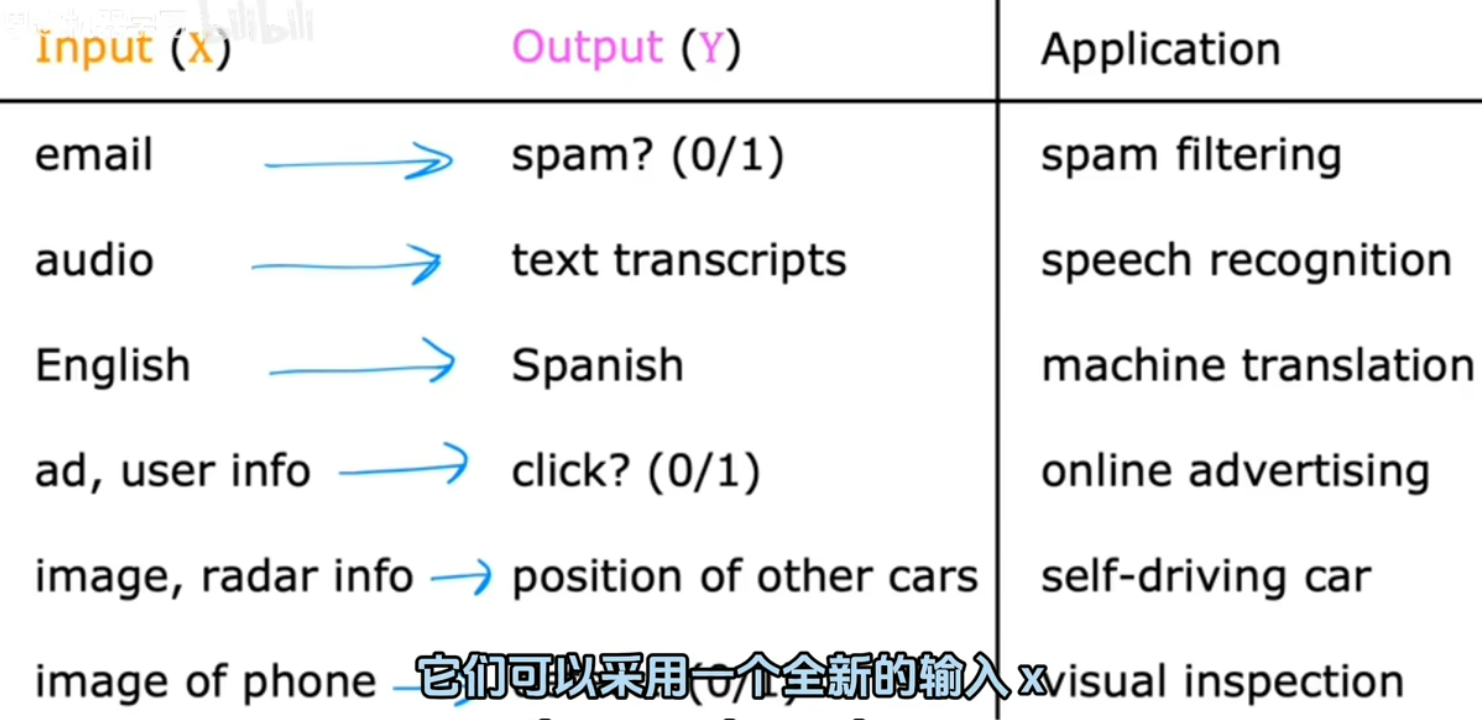
主要类型监督学习问题: 回归 分类
2.回归: 通过无数可能的数字中预测最可能的数字,例如房价预测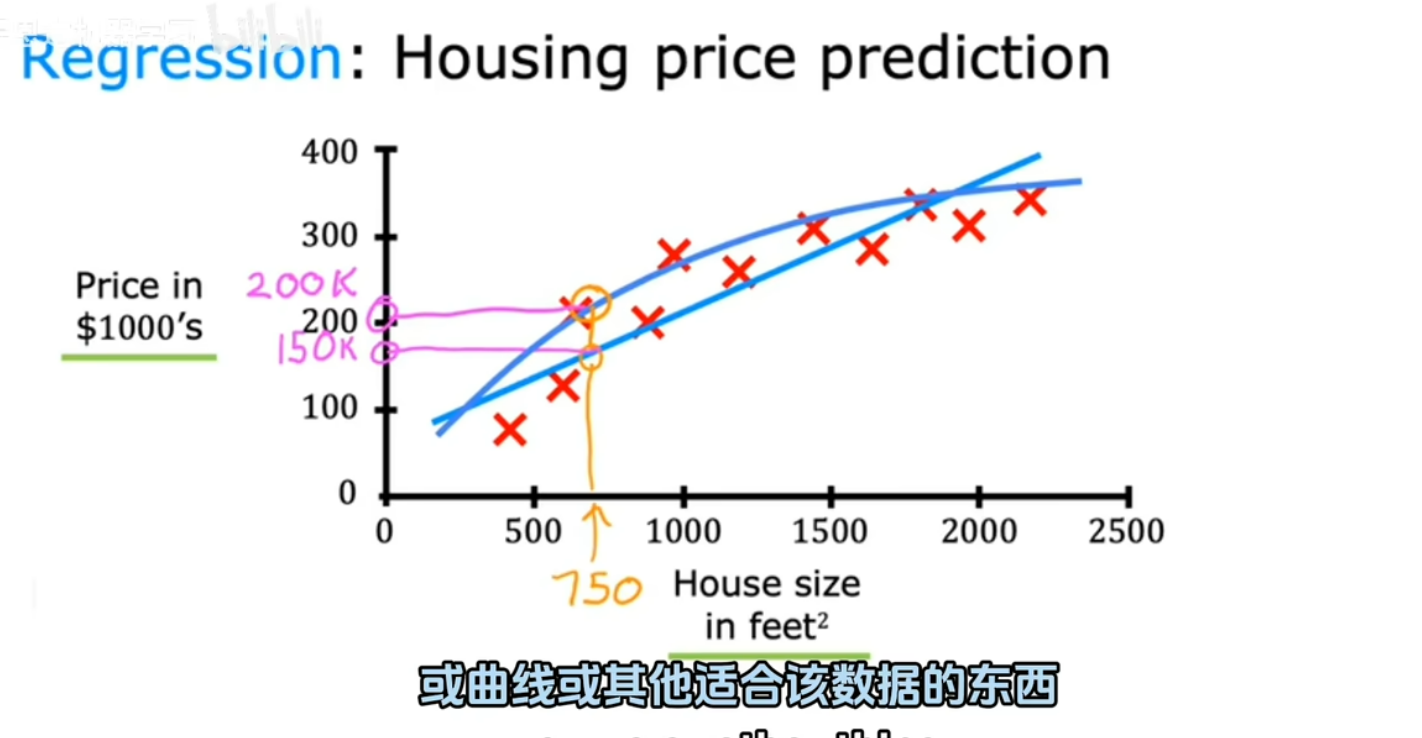
3.分类: 有限类别中进行分类,例如肿瘤预测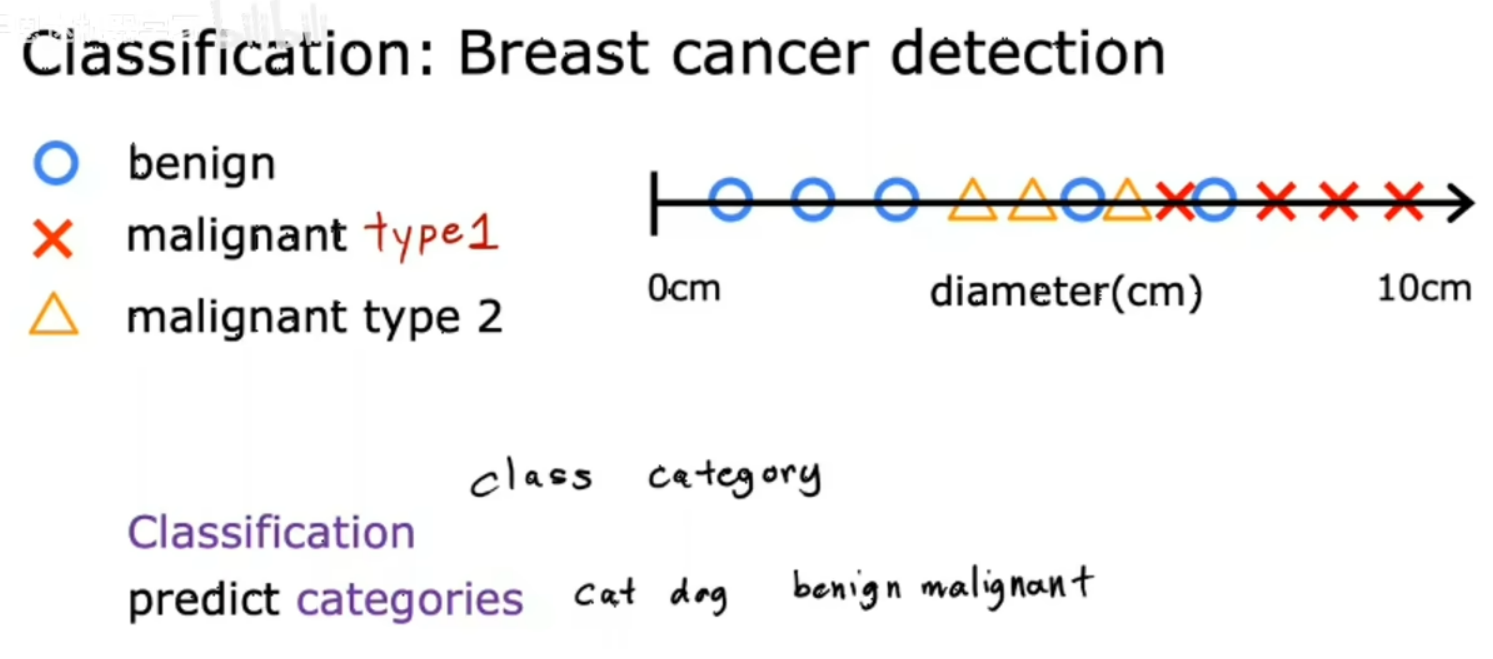
1.2.非监督学习
1.非监督学习: 仅有输入标签x 无输出标签y,在结构或模式中找到信息
主要类型非监督学习问题: 聚类 异常检测 降维
2.聚类:将未标记的数据放入不同的集群中 例如根据DNA将人分类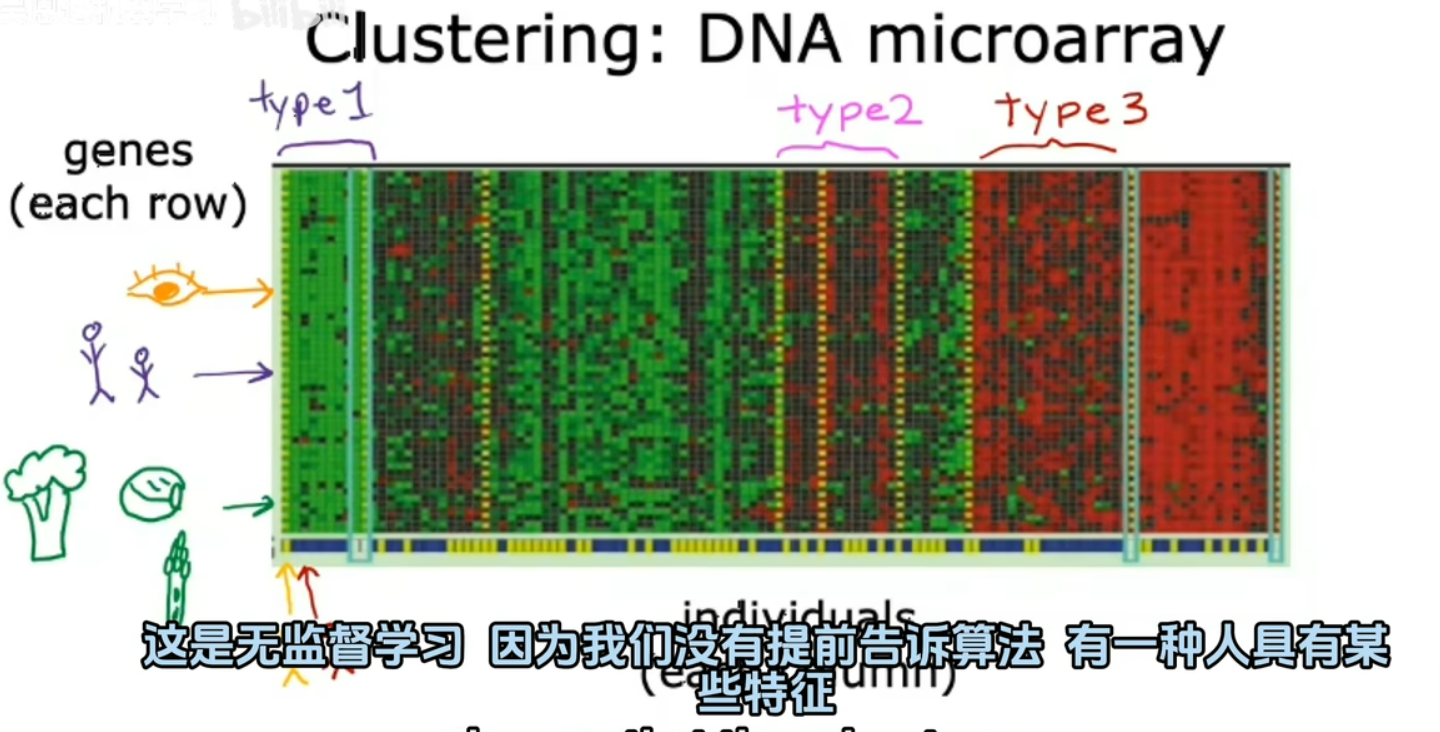
2.线性回归
2.1.线性回归模型
1.房价预测问题(单变量线性回归):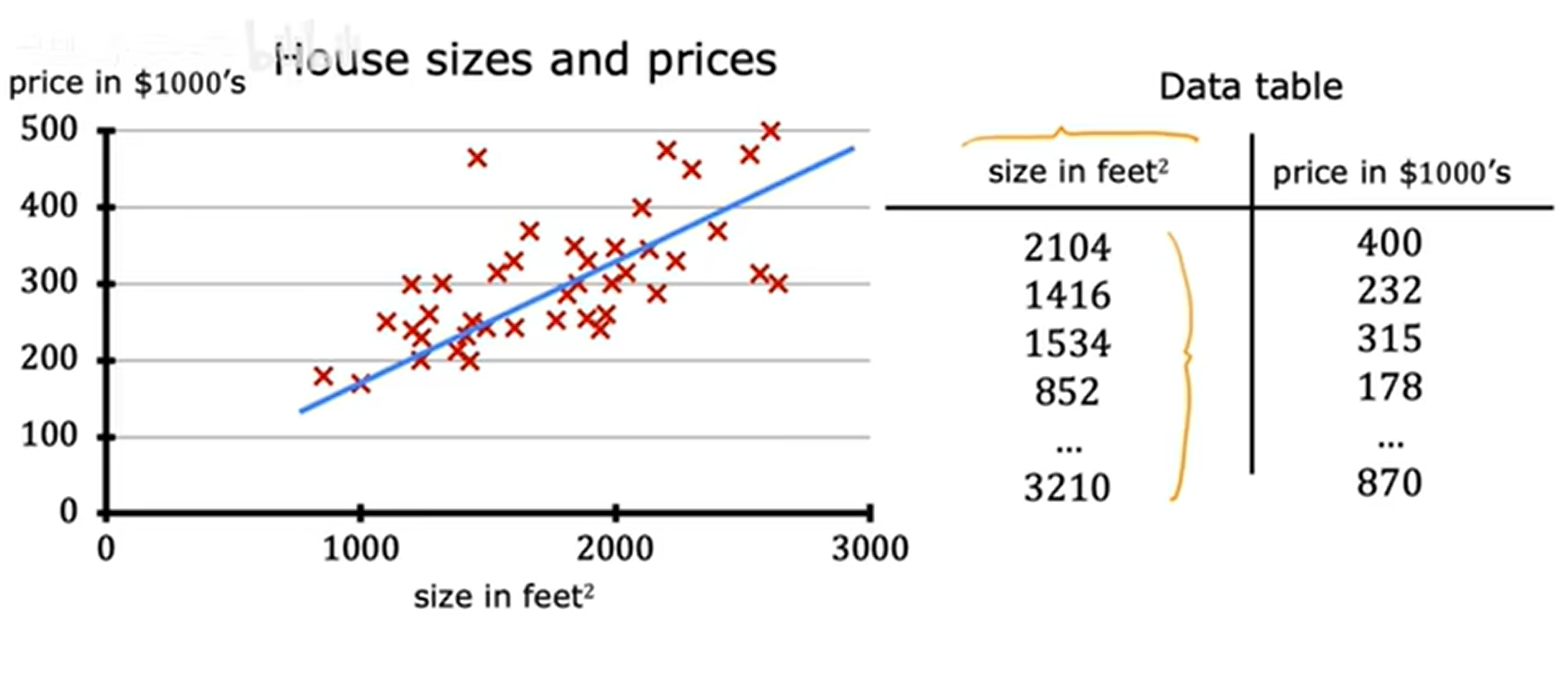
2.训练集: training assets 从训练集中训练模型后用模型进行预测
3.线性回归: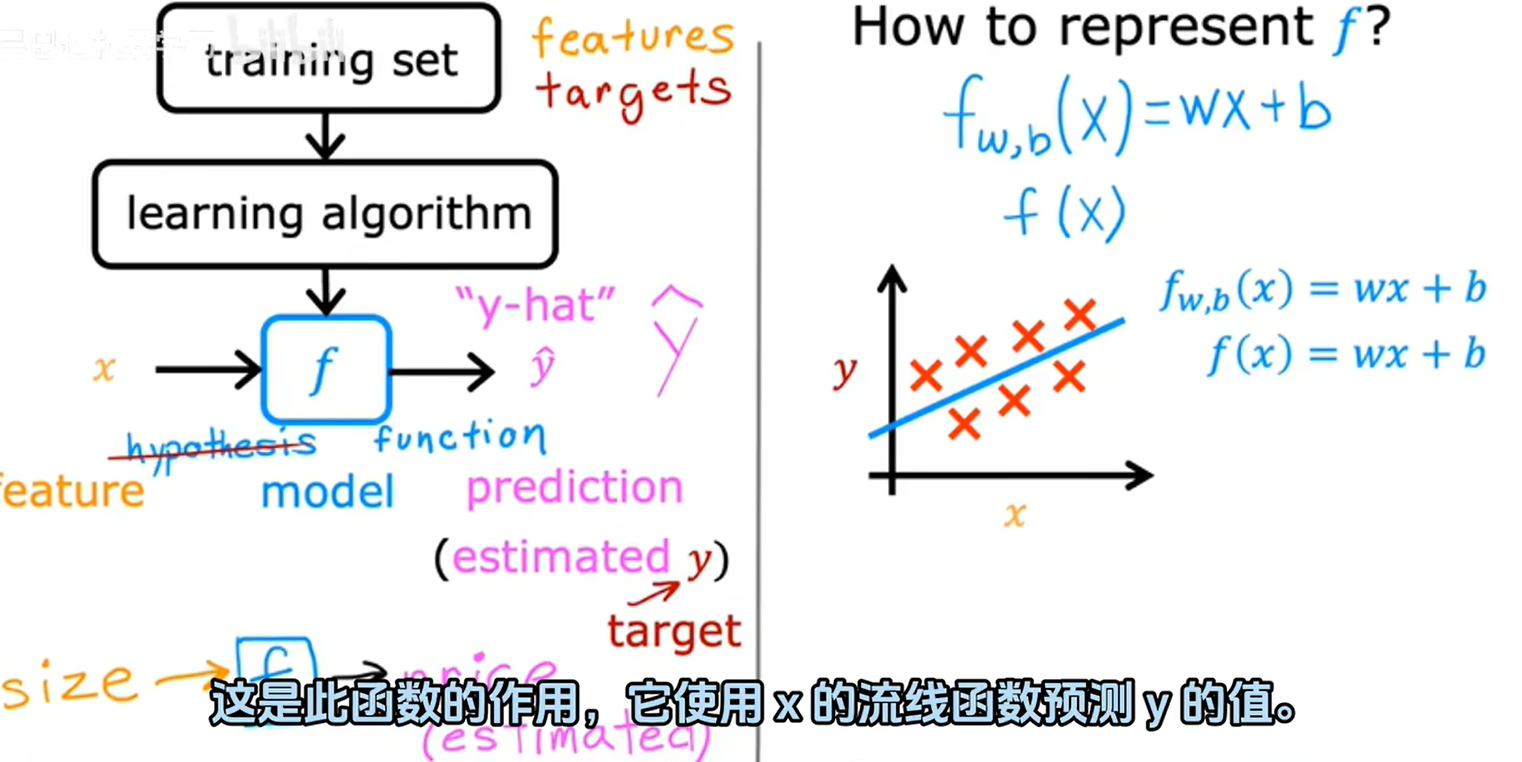
2.2.成本函数(代价函数)
1.成本函数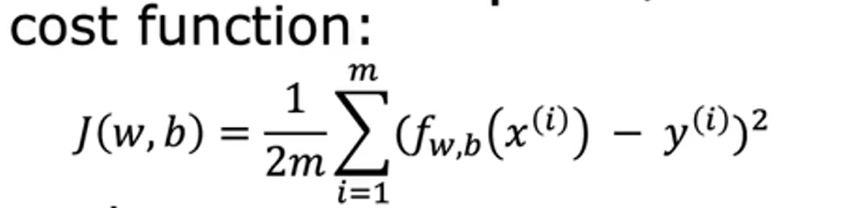
2.平方误差成本函数
3.fw(x)和J(w)
随着w该改变可以绘制出成本函数曲线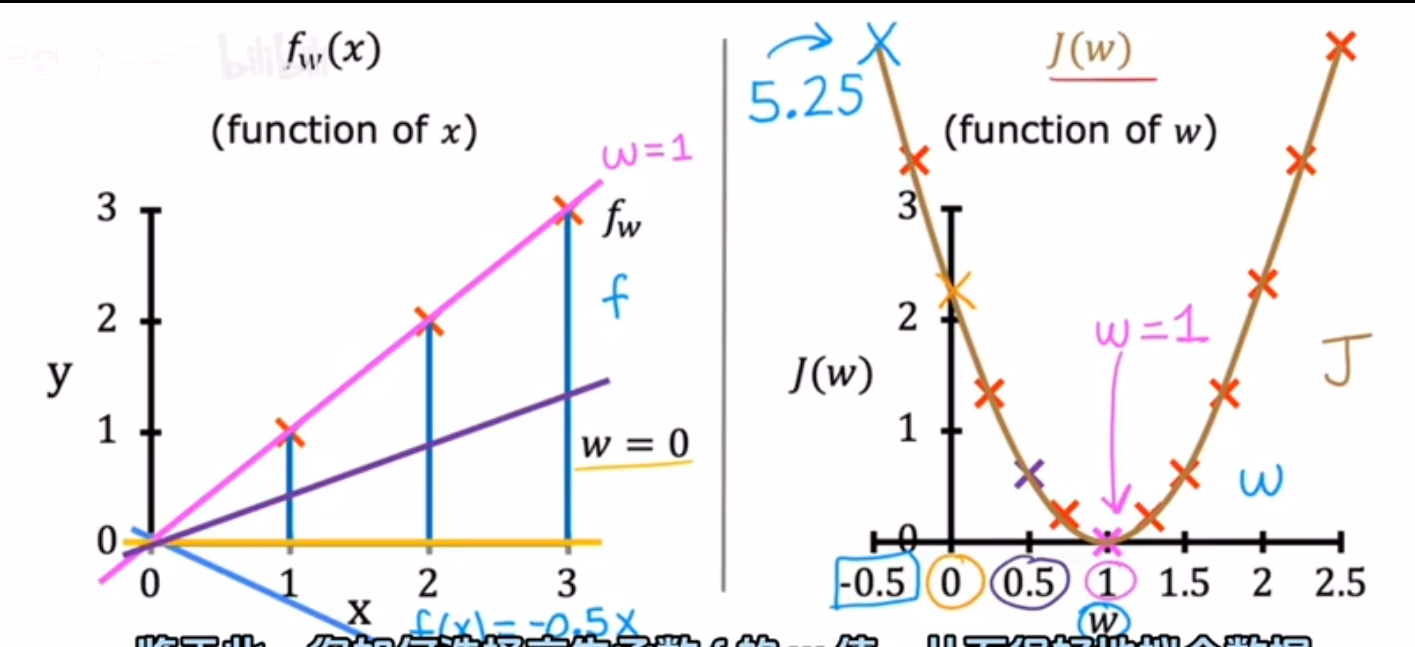
如上图当w=1效果最好
2.3.可视化代价函数
对于fw,b(x)和J(w,b) 可视化结果为3D曲面图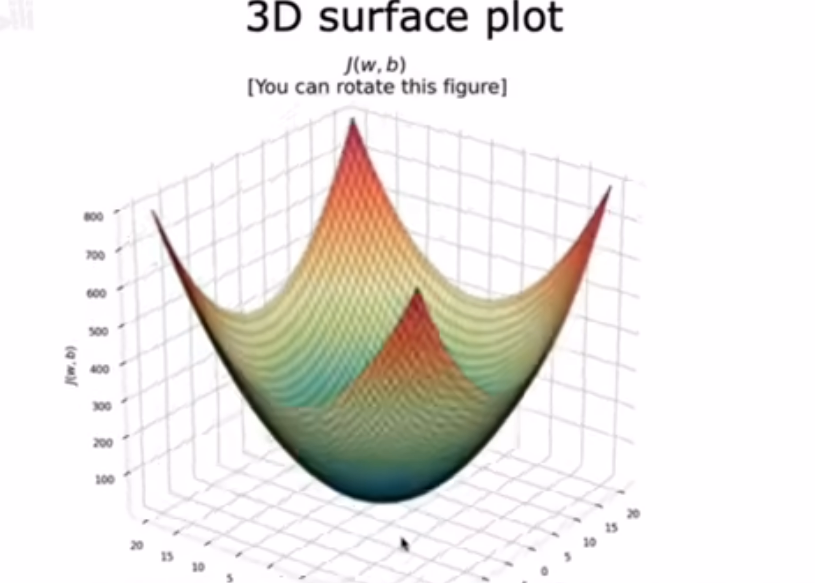
房价预测示例: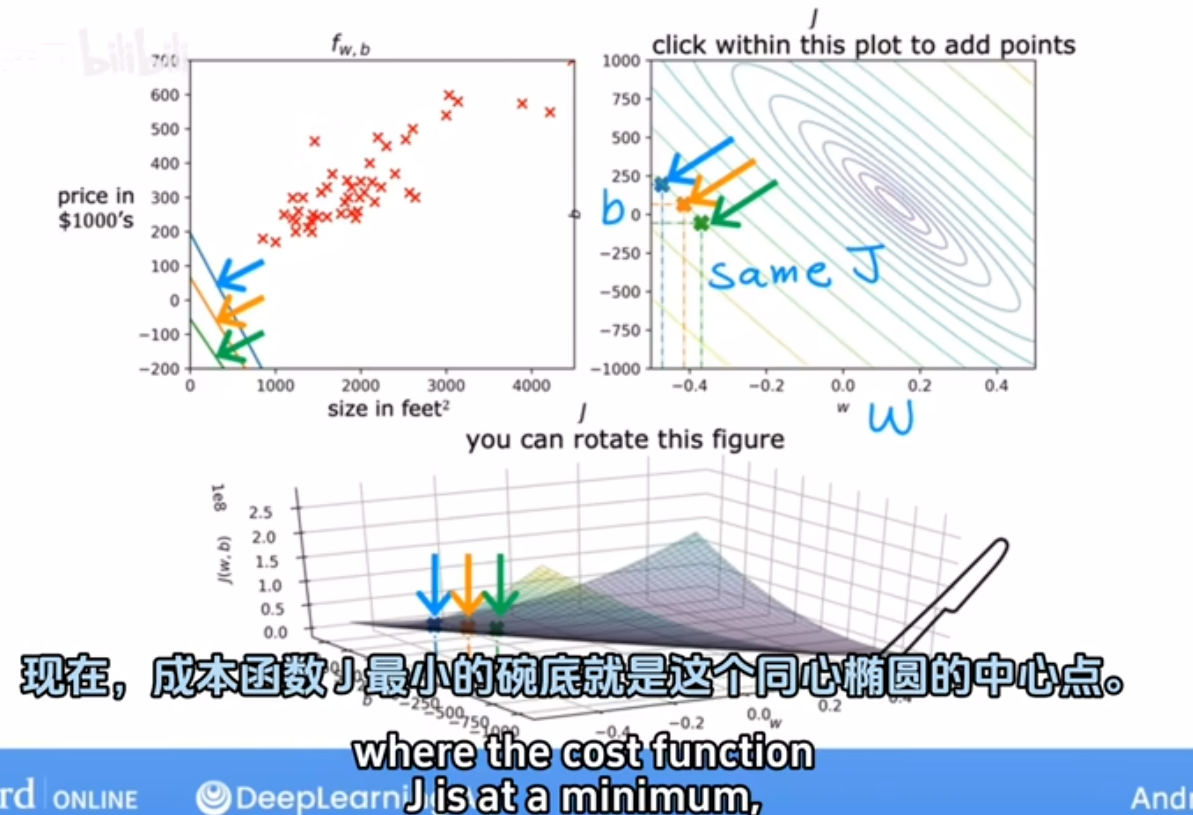
碗底最低点即成本函数最小,是同心椭圆的中心点
3.梯度下降
3.1.梯度下降介绍
1.梯度下降是一种可用于尝试最小化任何函数的算法。
某J(w,b)成本函数: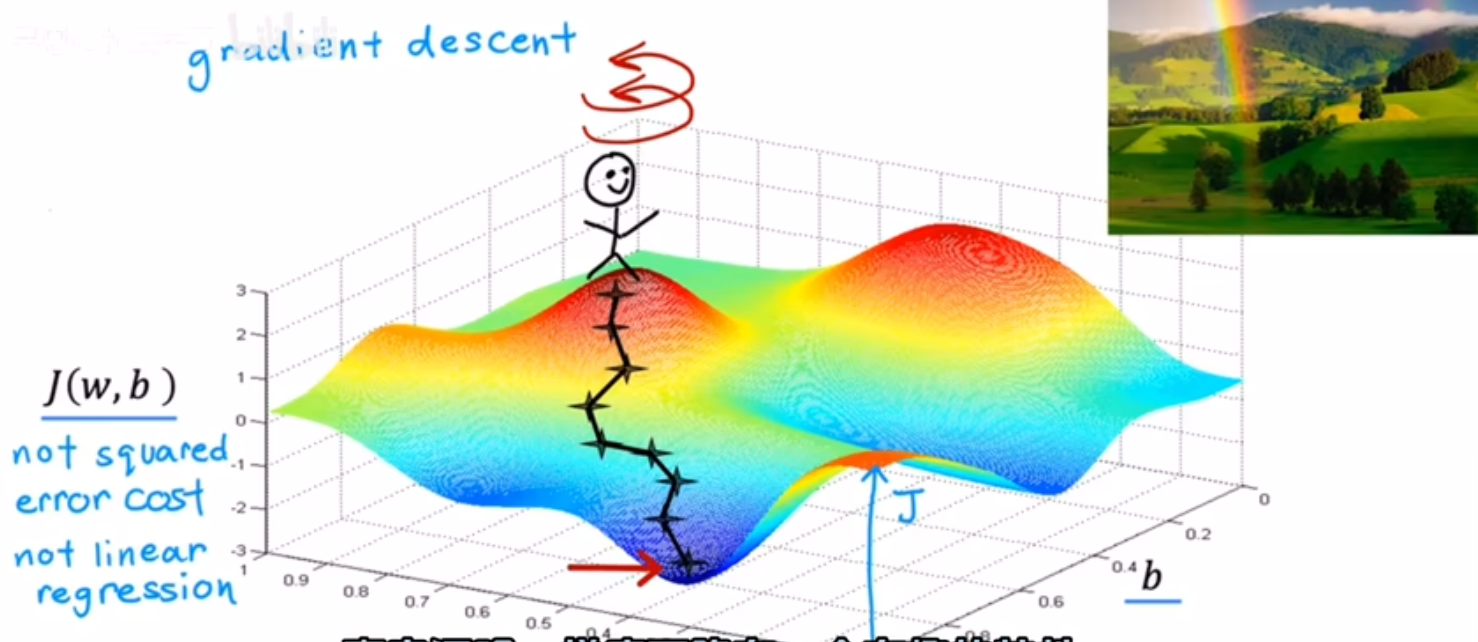
可以将成本函数看作山坡,位于一点时环视四周,不断找到坡度最陡的山坡(最速下降),最终到达低谷,这就是梯度下降的过程
2.起点不同可能到达的局部极小值不同:
例如从第一次的右侧几步作为起点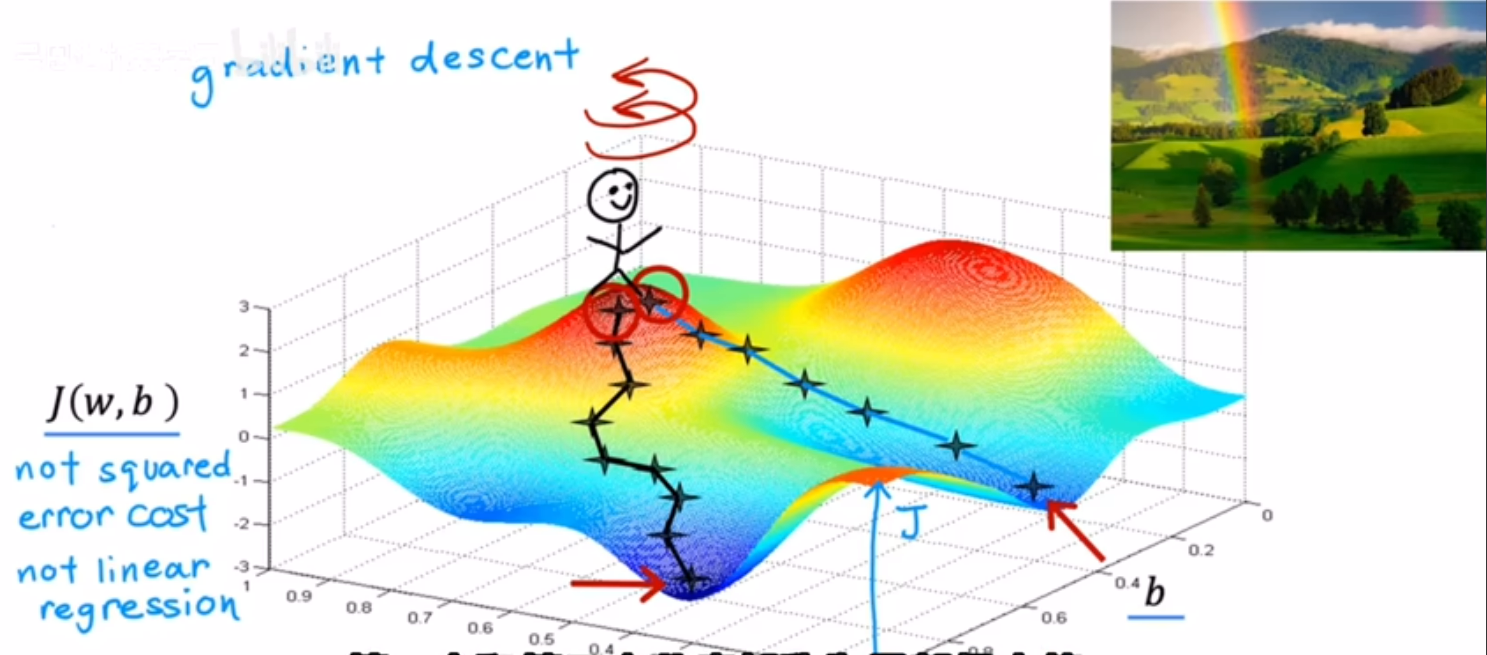
3.2.实现梯度下降
1.w公式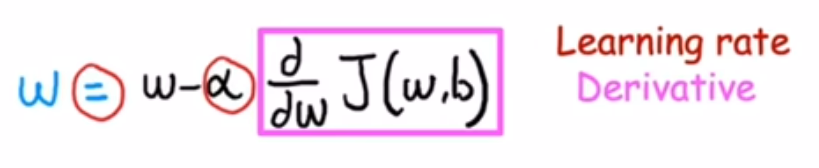
alpha:learning rate在梯度下降中控制你下坡的步幅,alpha大对应以巨大步骤下坡。
2.b公式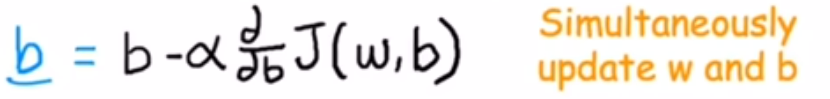
3.在梯度下降中将重复这两个公式直至收敛,到达局部最小值。其中参数w和b不再随着您采取的每个额外步骤而发生太大变化。
4.正确同步更新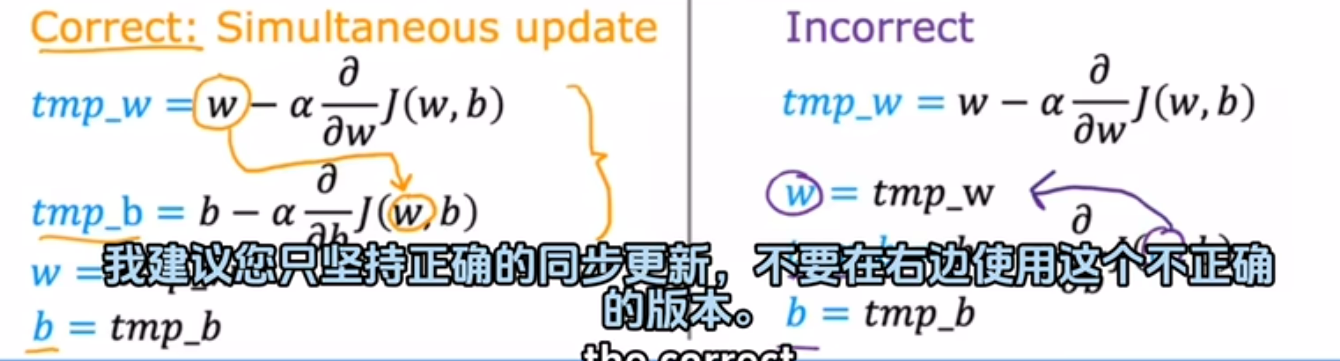
不采用同步更新可能会有一些影响,但这样做并不是真正正确的实现方式,实际上是其他一些具有不同属性的算法。
3.3.梯度下降实现的直观体现
只有w的线性函数实例: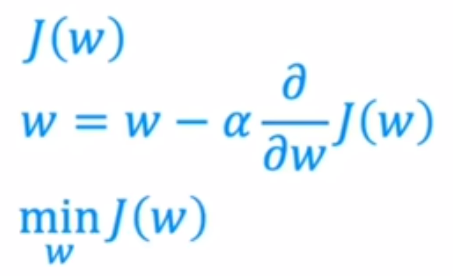 当w大于零即在对称轴右侧,经过算式后w变小,即往左移
当w大于零即在对称轴右侧,经过算式后w变小,即往左移
当w小于零即在对称轴左侧,经过算式后w变大,即往右移
总而言之都在想导数绝对值小的方向移动。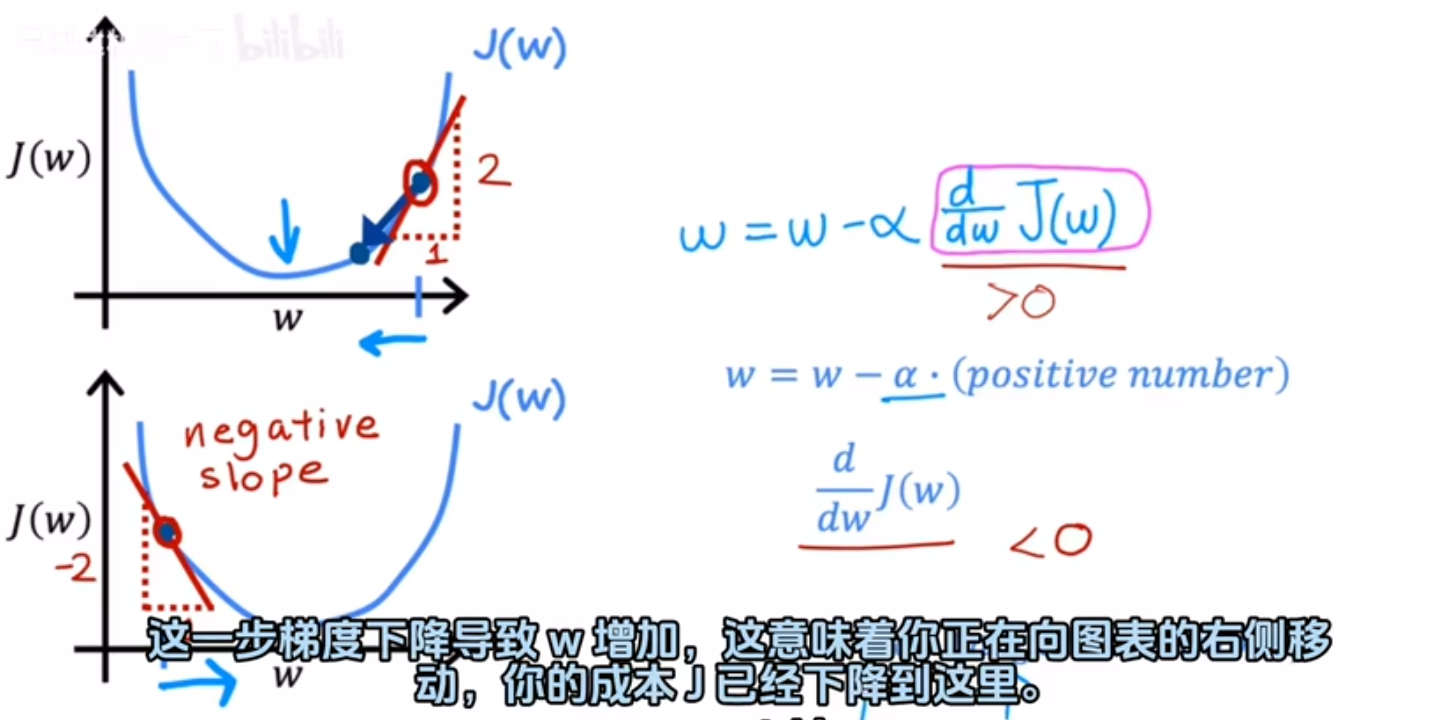
3.4.学习率
1.如果学习率很小,梯度下降会起作用,但是它很慢
2.如果学习率很大, 则梯度下降可能会过冲,并且可能永远不会达到最小值
3.初始点位于局部极小值的情况
当前点导数为0 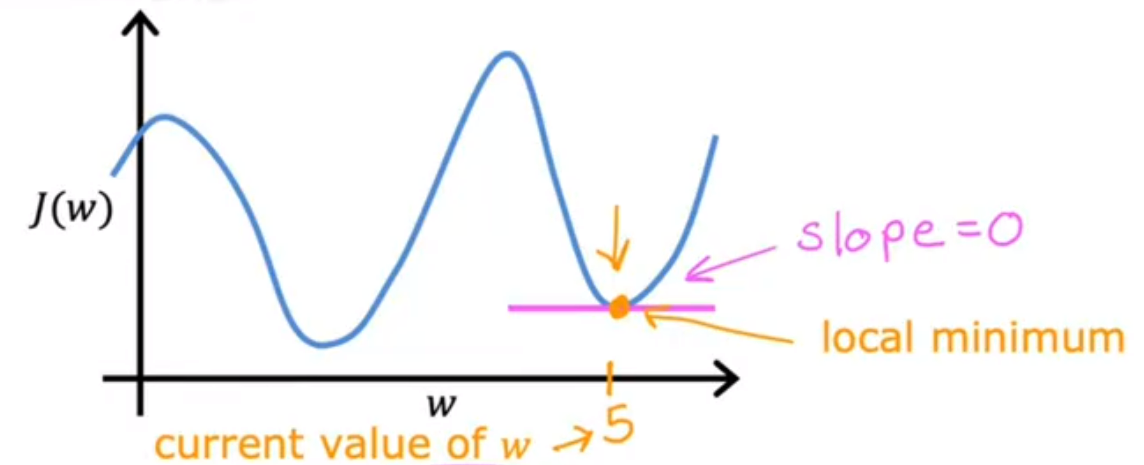 此时w不变
此时w不变
4.通过固定学习率值收敛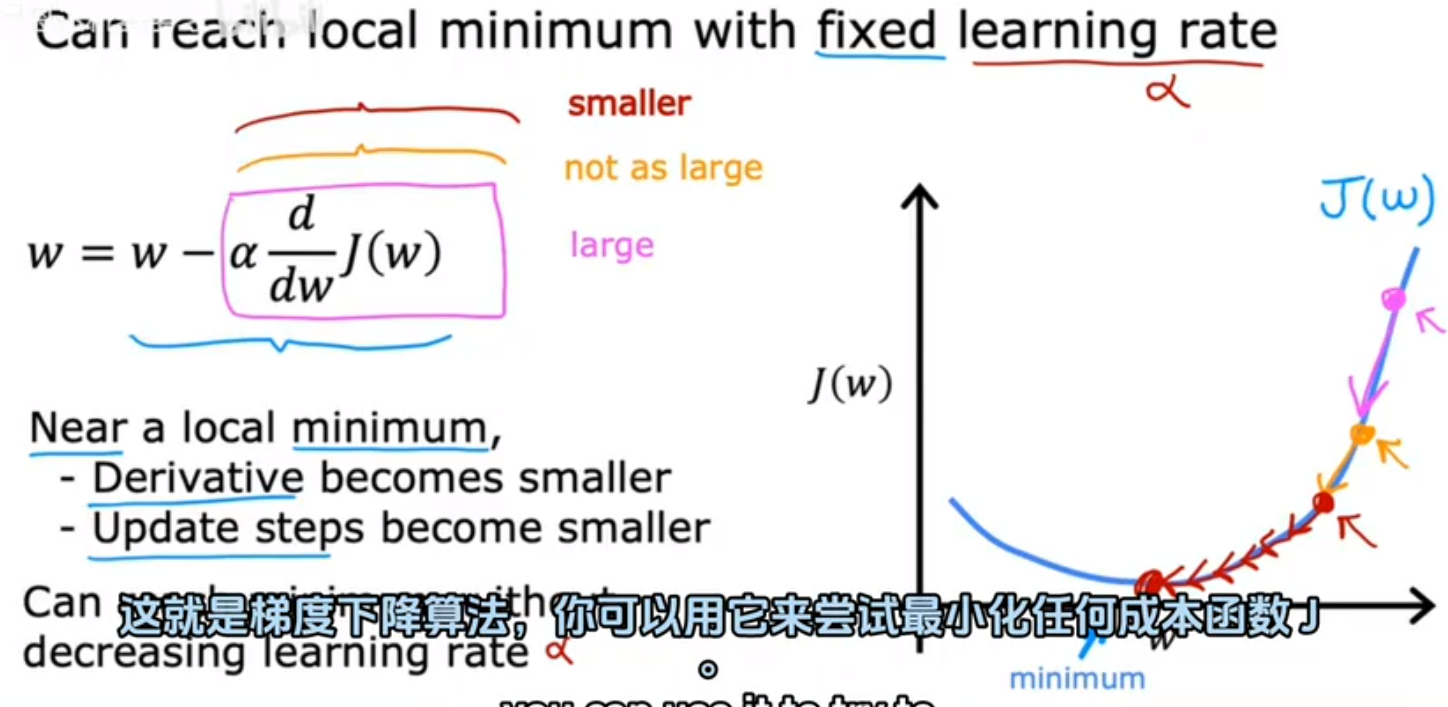 斜率越来越小,部署越来越小直至逼近局部极小值
斜率越来越小,部署越来越小直至逼近局部极小值
3.5.线性回归中的梯度下降
1.线性回归梯度下降涉及到的表达式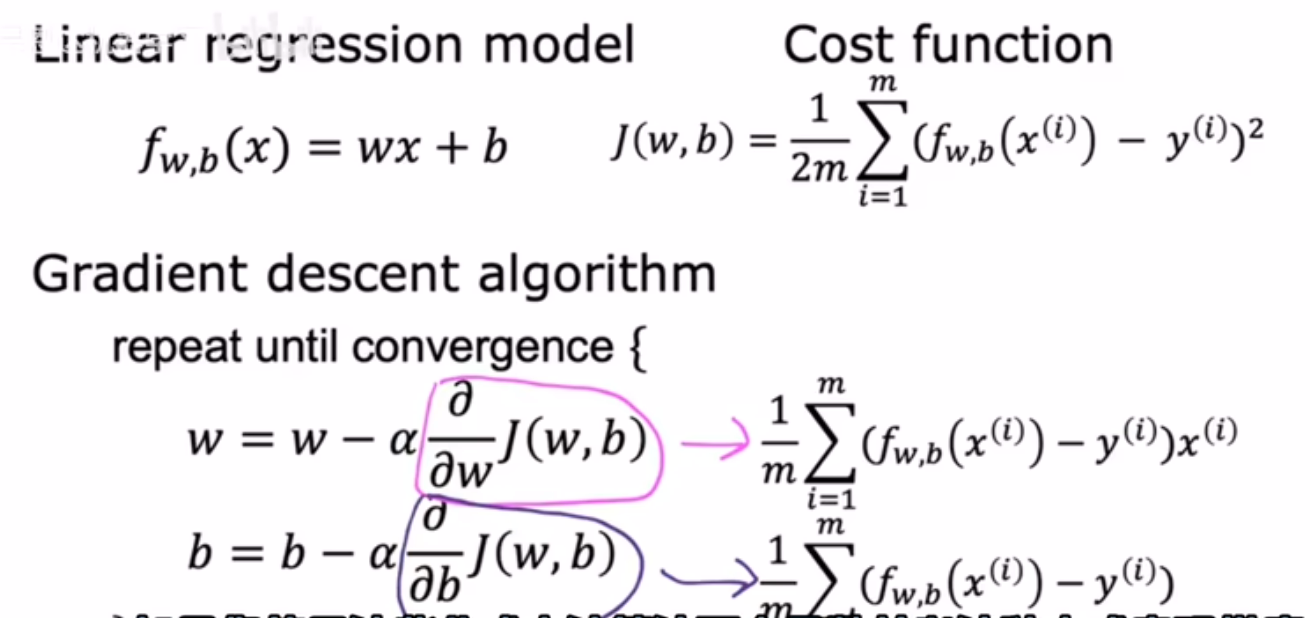 2.导数计算过程
2.导数计算过程 3.线性回归中的梯度下降过程
3.线性回归中的梯度下降过程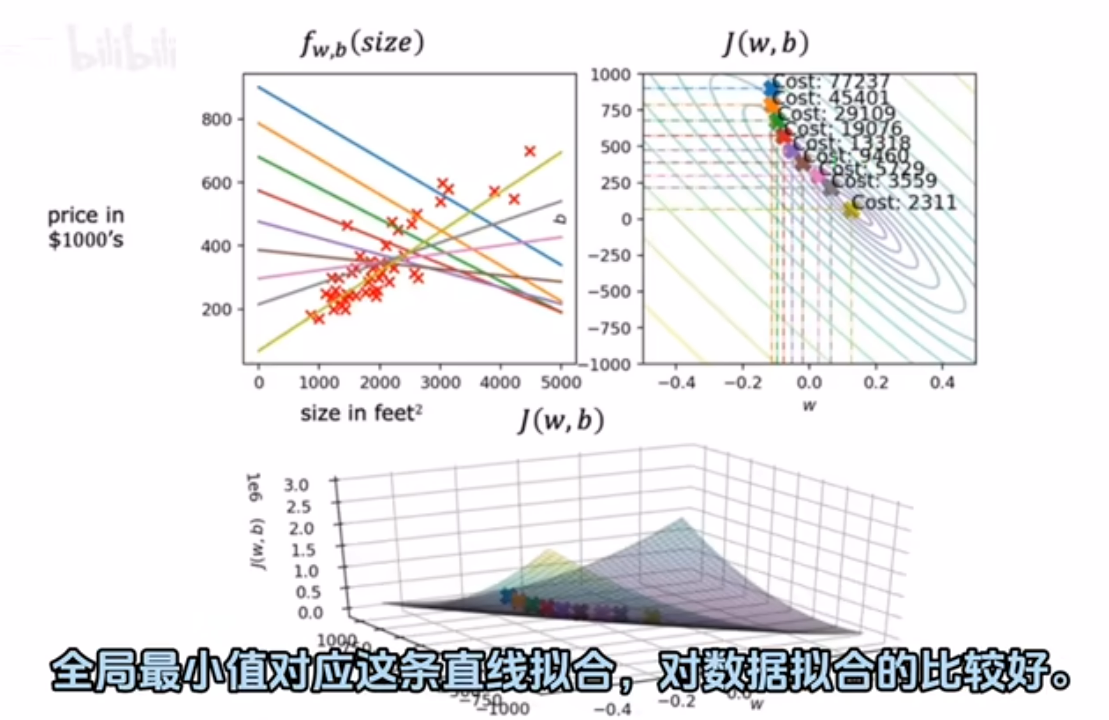 批量梯度下降: 梯度下降的每一步中我们都在查看所有的训练示例
批量梯度下降: 梯度下降的每一步中我们都在查看所有的训练示例
还有其他版本的梯度下降不会查看整个训练集,而是在每个更新步骤查看训练数据的较小子集。
4.多元化
4.1.多类特征
1.当x多元化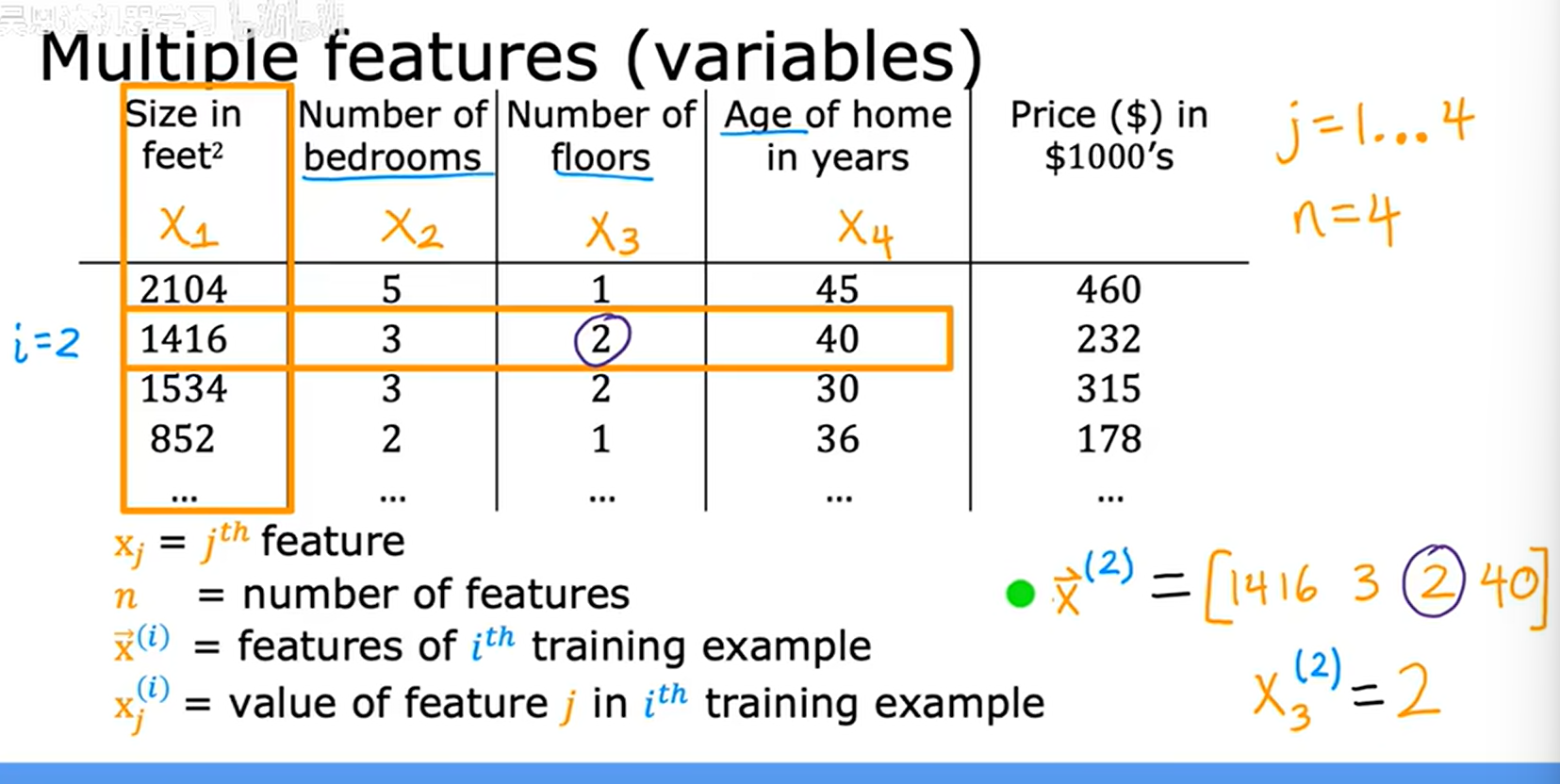 fw,b(x) = \w1\x1+ \w2\x2+\w3\x3+\w4\x4+b
fw,b(x) = \w1\x1+ \w2\x2+\w3\x3+\w4\x4+b
2.如果有n个feature
fw,b(x) = \w1\x1+ \w2\x2...+\wn\xn+b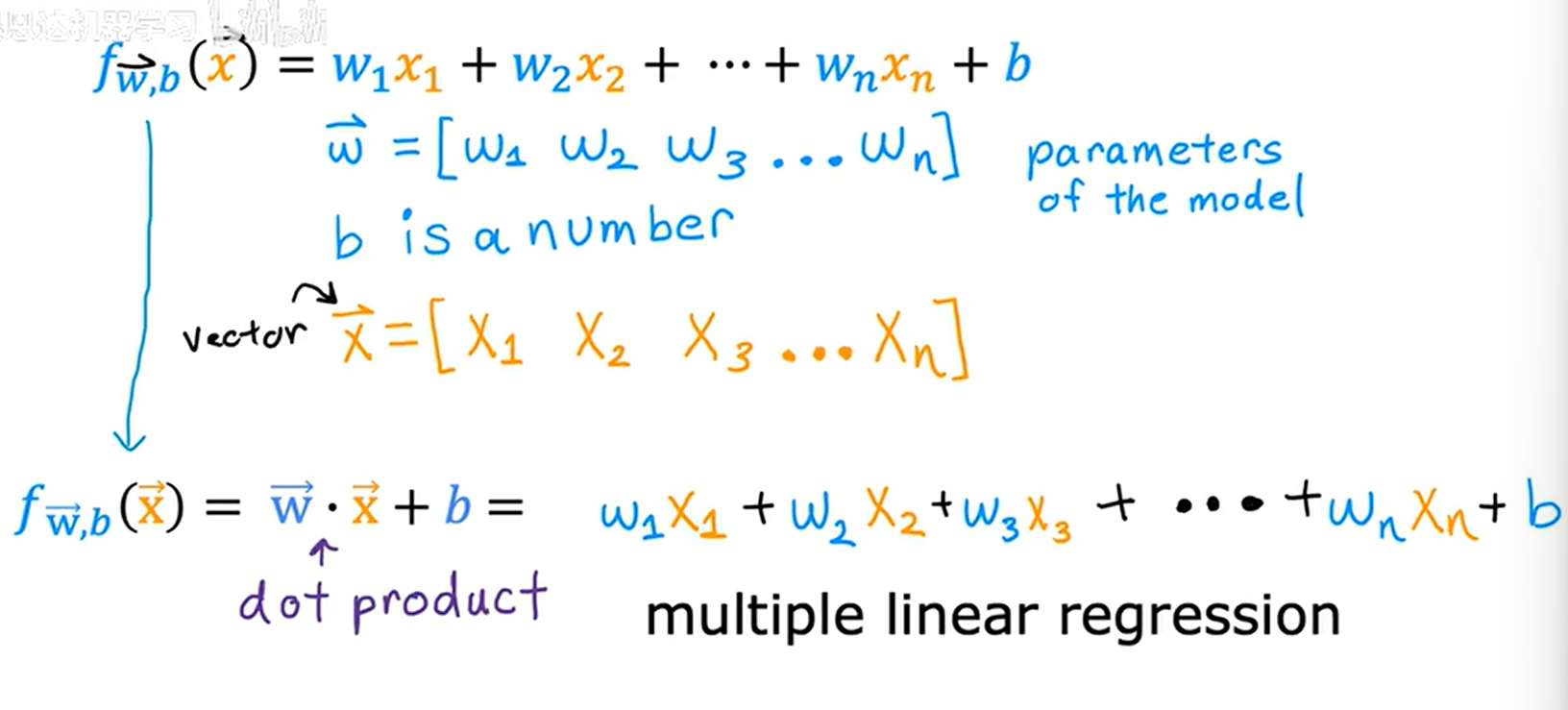
4.2.向量化
1.python的向量化应用(numpy) 向量化代码量更少,跑的更快(numpy函数能在计算机中使用并行硬件)
向量化代码量更少,跑的更快(numpy函数能在计算机中使用并行硬件)
2.numpy函数并行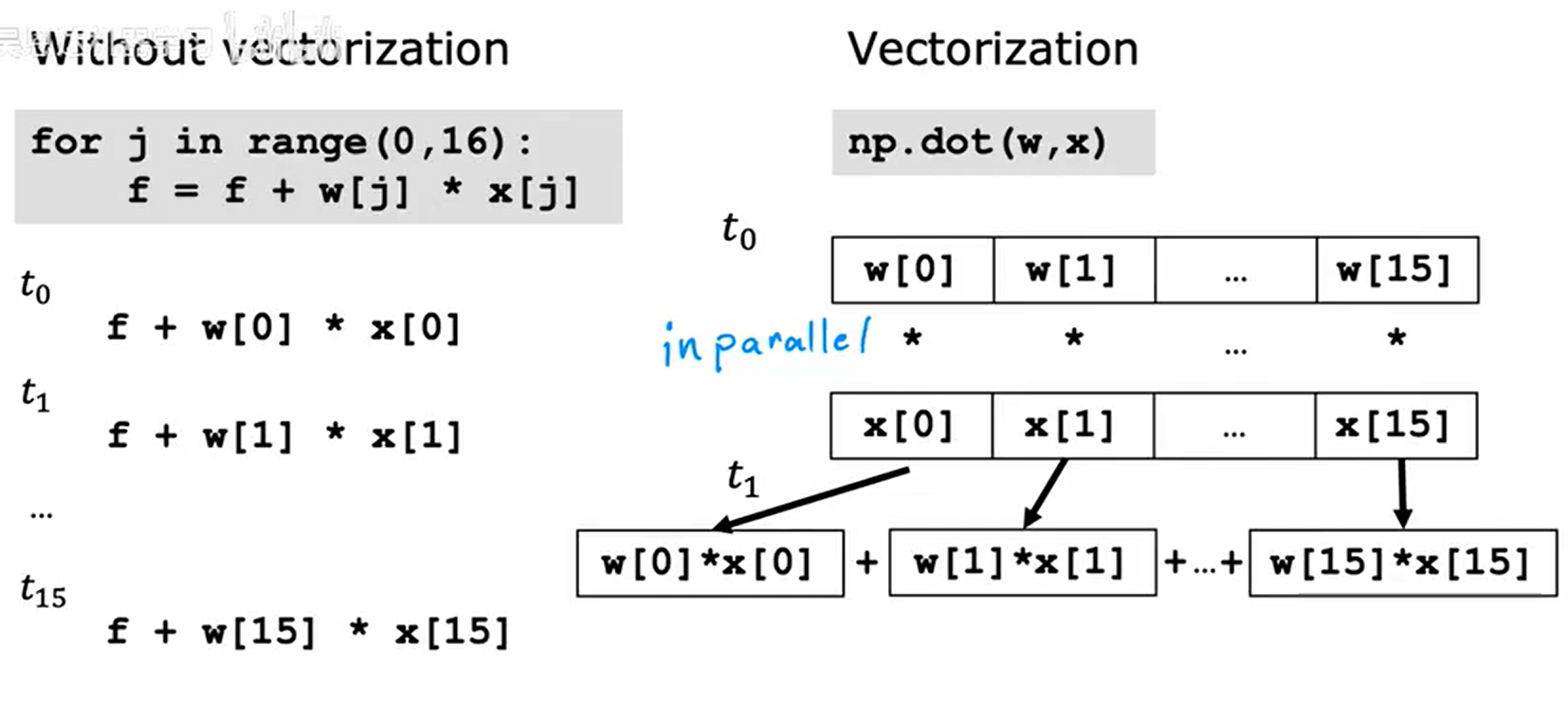 梯度下降并行
梯度下降并行
4.3多元线性回归的梯度下降算法
1.多元线性回归与单元对比
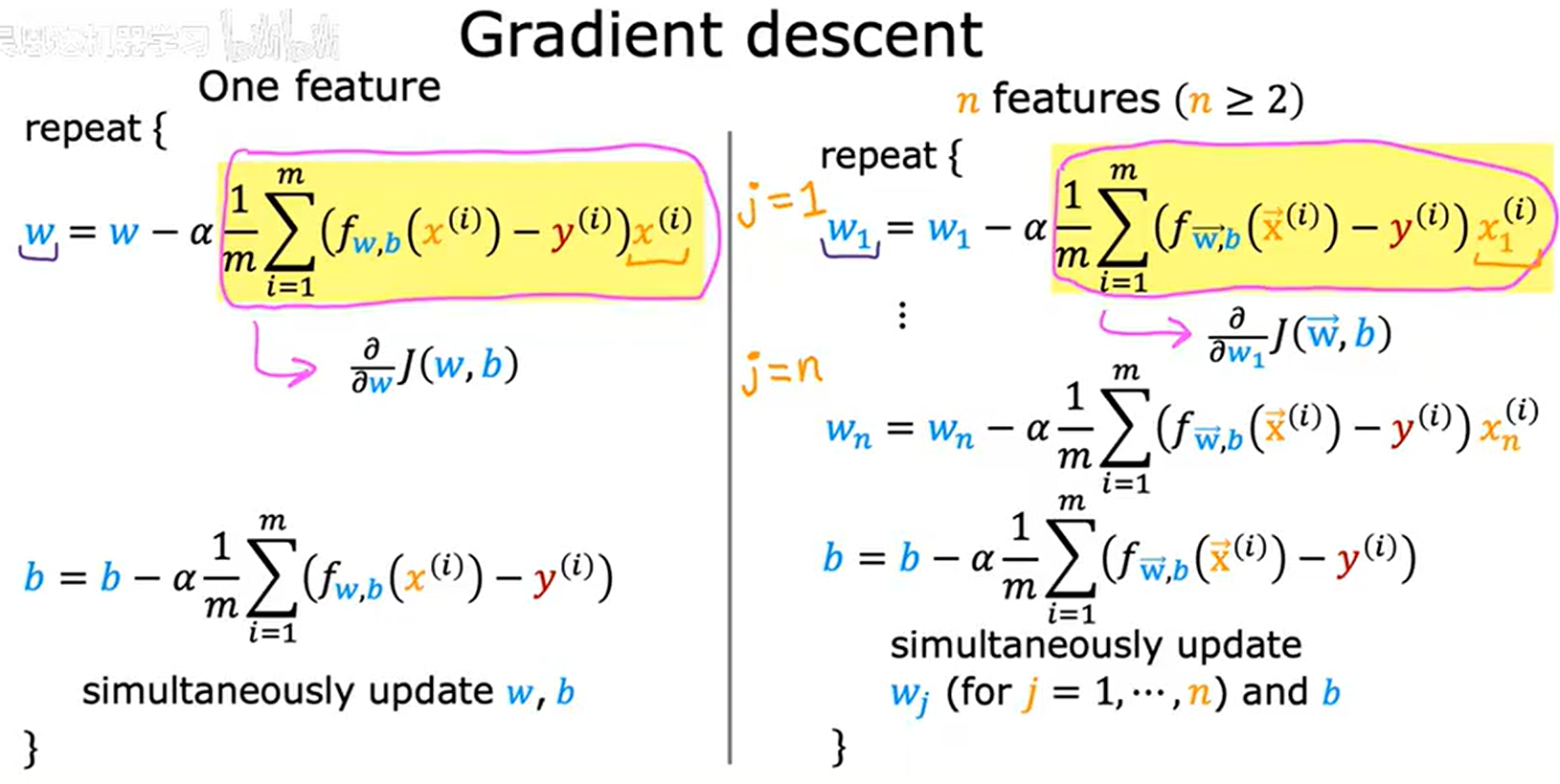
2.法方程降维
5.特征工程
5.1.特征缩放
1.不同参数对比 当x偏大时其前面的参数合理数值应当偏小,当x偏小时其前面的参数合理数值应当偏大
当x偏大时其前面的参数合理数值应当偏小,当x偏小时其前面的参数合理数值应当偏大
2.特征大小对梯度下降的影响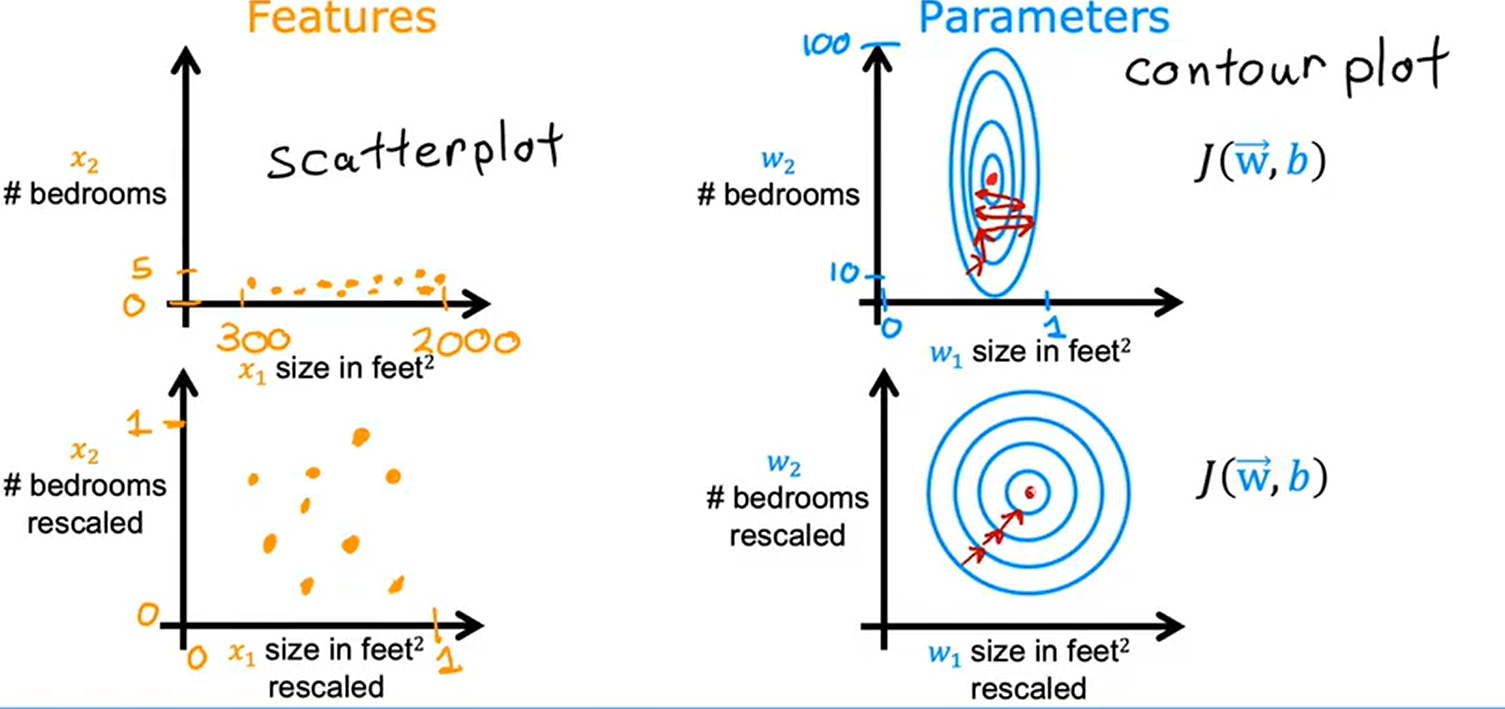 未经过特征缩放梯度下降找到局部极小值较难
未经过特征缩放梯度下降找到局部极小值较难
经过特征缩放梯度下降可以找到更直接的路径到达局部极小值
5.2.缩放方法
1.归一化缩放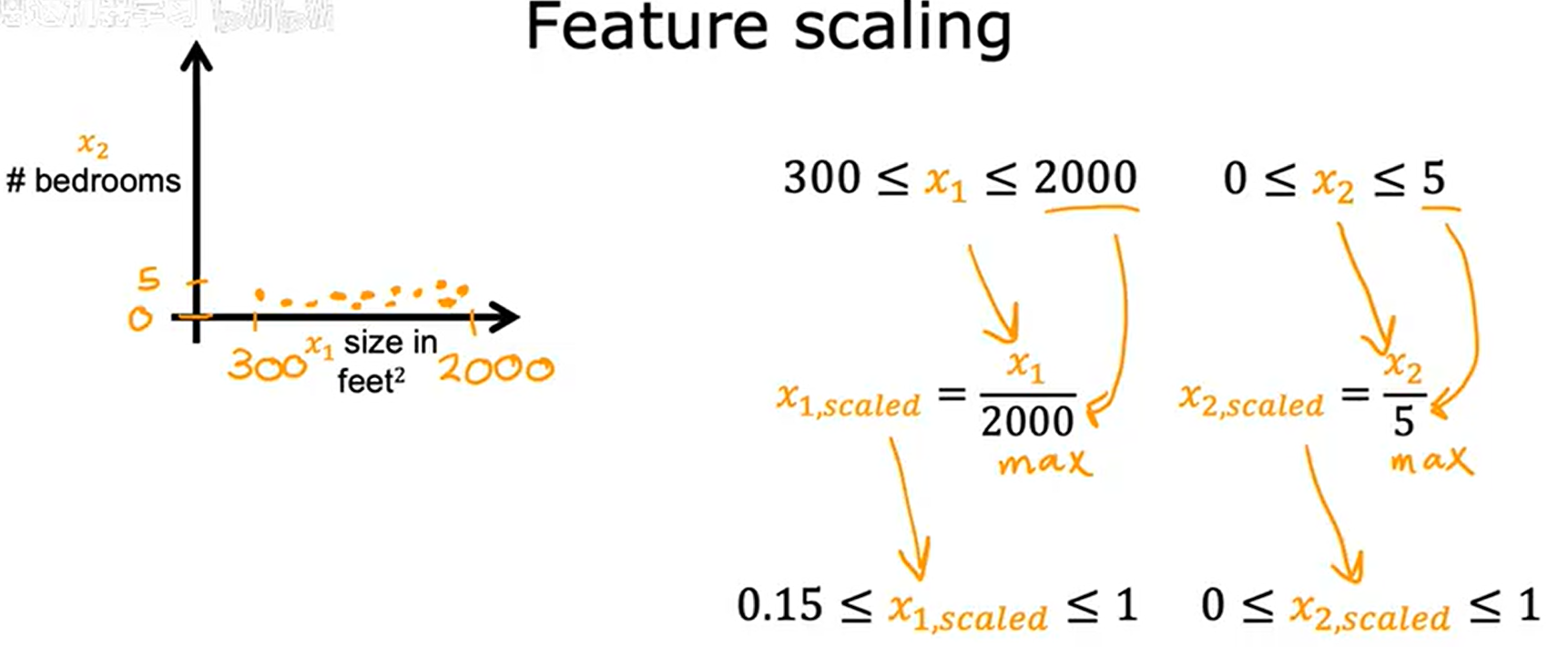
2.K均值缩放
3.Z-score缩放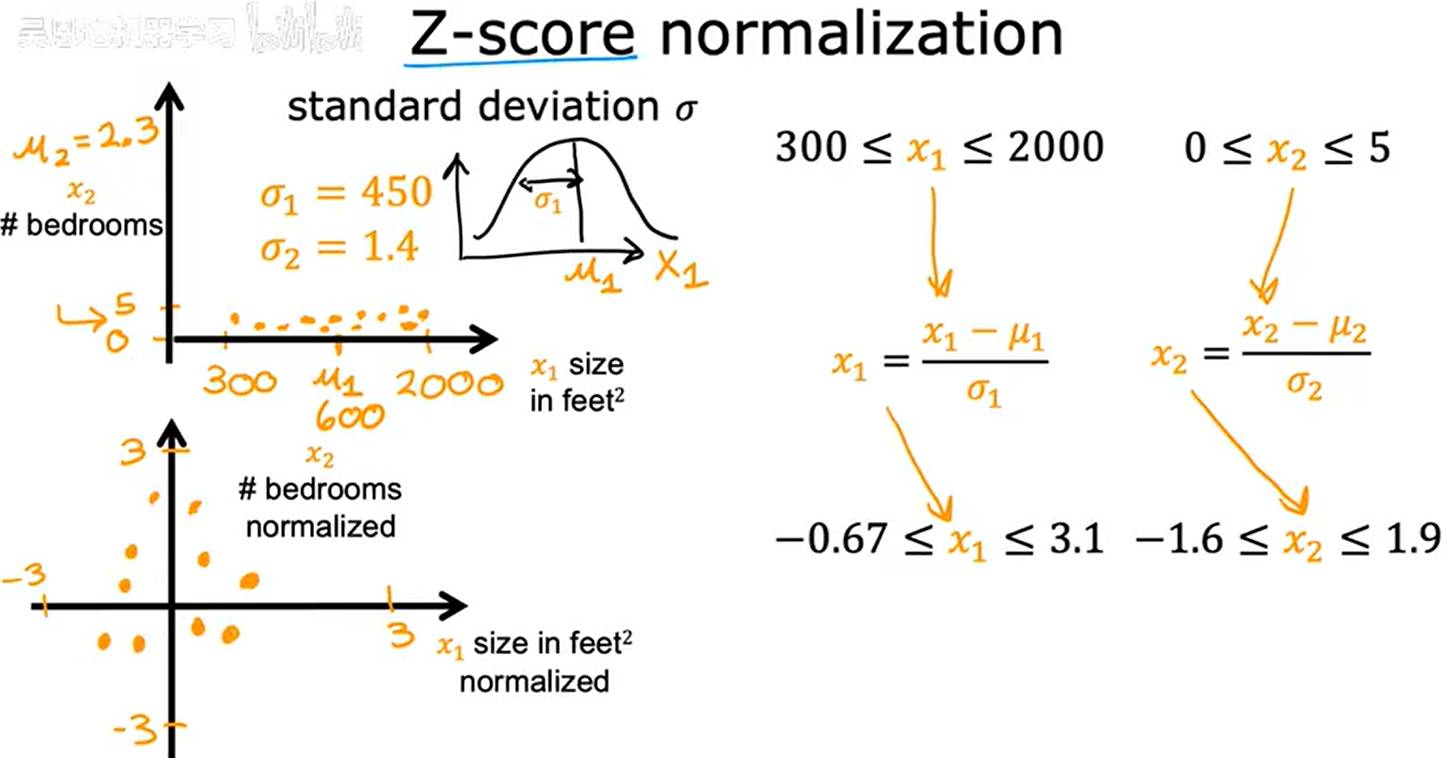
4.当缩放结果过小或过大时应当重新缩放。






