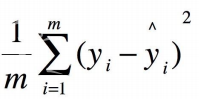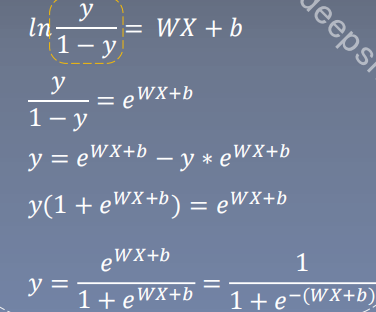深度学习基础

学习视频:https://www.bilibili.com/video/BV1zS4y1n7Eq/?spm_id_from=333.1007.top_right_bar_window_history.content.click

1.Pytorch基础概念

1.Pytorch安装

运行

nvidia-smi

查看cuda版本，去官网下载对应版本cuda

CUDNN安装:https://developer.nvidia.com/cudnn
Pytorch安装:https://pytorch.org/
pip安装:https://download.pytorch.org/whl/torch_stable.html
下载的torch与torchvision版本需对应
例如 Windows+python 3.8环境下

https://download.pytorch.org/whl/cu116/torchvision-0.14.0%2Bcu116-cp38-cp38-win_amd64.whl
https://download.pytorch.org/whl/cu116/torch-1.12.0%2Bcu116-cp38-cp38-win_amd64.whl

下载完成后放到同一个文件夹中

conda

//conda创建虚拟环境
conda create -n [环境名] python=3.8
//激活虚拟环境
conda activate [环境名]
//进入存放torch和torchvisionwhl文件的目录中
cd [文件目录路径]
//安装torch
pip install "torch文件名.whl"
//安装torchvision
pip install "torchvision文件名.whl"

pycharm设置
File->Settings->Project下的Python Interpreter中加入conda环境的解释器

设置完成后运行

import torch  
  
print("Hello torch {}".format(torch.__version__))
print(torch.cuda.is_available())

成功输出版本

Hello torch 1.13.0+cpu
True

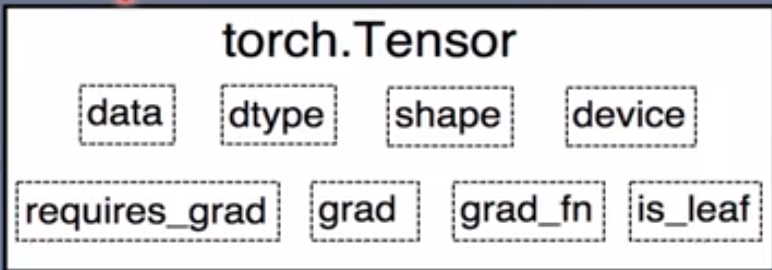
2.Tensor张量

1.张量概念

张量是一个多维数组，它是标量、向量、矩阵的高维拓展。
Variable是Pytorch0.4.0前的数据类型，是torch.autograd中的数据类型，用于封装Tensor进行自动求导。

data:被封装的Tensor
grad:data的梯度
grad_fn: 创建Tensor的Function,是自动求导的关键
requires_grad: 指示是否需要梯度
is_leaf: 指示是否是叶子结点(张量)
dtype:张量的数据类型
shape:张量的形状
device:张量所在设备

2.创建张量

1.直接创建

• torch.tensor()

  torch.tensor(
  	data,
  	dtype=None,
  	device=None,
  	requires_grad=False,
  	pin_memory=False
  )
  data:数据，可以是list,numpy
  dtype:数据类型
  device:所在设备
  requires_grad: 是否需要梯度
  pin_memory: 是否存于锁页内存
  
  #实例
  import torch
  import numpy as np
  flag = True
  if flag:
      arr = np.ones((3, 3))
      print("ndarray数据类型", arr.dtype)
      t = torch.tensor(arr, device="cuda")
      print(t)

• torch.from_numpy(ndarray)
  从numpy创建tensor,从该函数创建的tensor与原ndarray共享内存,修改其中一个的数据，另一个也将会被改动

2.依据数值创建

• torch.zeros()

  torch.zeros(*size,
  	out=None,
  	dtype=None,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )
  
  size:张量的形状
  out:输出的张量
  layout:内存中布局形式，有strided,sparse_coo等
  device:所在设备
  requires_grad:是否需要梯度
  
  #实例
  out_t = torch.tensor([1])
  t = torch.zeros((3, 3), out=out_t)
  print(t, "\n", out_t)
  print(id(t), id(out_t), id(t) == id(out_t))
  #tensor([[0, 0, 0],
  #        [0, 0, 0],
  #        [0, 0, 0]])
  # tensor([[0, 0, 0],
  #        [0, 0, 0],
  #        [0, 0, 0]])
  #2750875670976 2750875670976 True
  两者同一内存空间

• torch.zeros_like()
  依input形状创建全0张量

  torch.zeros_like(input,
  	dtype=None,
  	layout=None,
  	device=None,
  	requires_grad=False
  )
  
  input:创建与input同形状的全0张量
  dtype:数据类型
  layout:内存中的布局形式

• torch.ones() torch.ones_like()同理
• torch.full()

  torch.full(size,
  	fill_value,
  	dtype=None,
  	out=None,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )
  
  size:张量的形状如(3,3)
  fill_value:张量的值
  #实例
  t = torch.full((3, 3), 10)
  print(t)

• torch.arange()
  功能:创建等差的1维张量 数值区间为左闭右开[start,end)

  torch.arange(start=0,
  	end,
  	step=1,
  	out=None,
  	dtype=None,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )
  start:数列起始值
  end:数列"结束值"
  step:数列公差，默认为1
  
  #实例
  t = torch.arange(2, 10, 2)
  print(t)
  #tensor([2, 4, 6, 8])

• torch.linspace()
  功能:创建均分的1维张量，数值区间为[start,end]

  torch.linspace(start,
  	end,
  	steps=100,
  	out=None,
  	dtype=None,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )
  start:数列起始值
  end:数列结束值
  steps:数列长度
  
  #实例
  t = torch.linspace(2, 10, 6)
  print(t)
  #tensor([ 2.0000,  3.6000,  5.2000,  6.8000,  8.4000, 10.0000])

• torch.logspace()
  功能:创建对数均分的1维张量，长度为steps,底为base

  torch.logspace(start,
  	end,
  	steps=100,
  	base=10.0,
  	out=None,
  	dtype=None,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )
  start:数列起始值
  end:数列结束值
  steps:数列长度
  base:对数函数的底，默认为10

• torch.eye()
  创建单位对角矩阵(二维张量)

  torch.eye(n,
  	m=None,
  	out=None,
  	dtype=None,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )
  n:矩阵行数，默认只设置行数
  m:矩阵列数

3.依概率分布创建张量

• torch.nomal()
  生成正态分布(高斯分布)

  torch.normal(mean,
  	std,
  	out=None
  )
  mean:均值
  std:标推差 
  两者均可为向量或标量
  #实例
  flag = True
  if flag:
      #均标量，用size控制生成张量大小
      t_normal = torch.normal(0.,1.,size=(4,))
      print(t_normal)
      #张量标量
      mean = torch.arange(1,5,dtype=torch.float)
      std = 1
      t_normal = torch.normal(mean,std)
      print("mean:{}\nstd:{}".format(mean,std))
      print(t_normal)

• torch.randn()标准正态分布

• torch.randn_like()生成标准正态分布，设置size即可

• torch.rand()生成均匀分布

• torch.rand_like() 在区间[0,1)上，生成均匀分布

• torch.randint()

• torch.randint_like()功能:区间[low,high)生成整数均匀分布，size:张量形状

• torch.randperm()
  功能:生成从0到n-1的随机排列
  n:张量的长度

  torch.randperm(n,
  	out=None,
  	dtype=torch.int64,
  	layout=torch.strided,
  	device=None,
  	requires_grad=False
  )

• torch.bernoulli
  功能:以input为概率，生成伯努利分布

  torch.bernoulli(input,
  	*,
  	generator=None,
  	out=None
  )

3.张量操作

1.拼接与切分

1.torch.cat()将张量按维度dim进行拼接

torch.cat(tensors, #张量序列
	dim=0,  #需要拼接的维度
	out=None
)

#实例
t = torch.ones((2, 3))
t_0 = torch.cat([t, t], dim=0)
t_1 = torch.cat([t, t], dim=1)
print("t_0:{} shape:{}\nt_1:{} shape:{}".format(t_0, t_0.shape, t_1, t_1.shape))

#res
t_0:tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]]) shape:torch.Size([4, 3])
t_1:tensor([[1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1.]]) shape:torch.Size([2, 6])

2.torch.stack() 在新创建的维度dim上进行拼接

torch.stack(tensors,
	dim=0, #新创建的维度上进行拼接
	out=None
)


#实例
t = torch.ones((2, 3))
t_test = torch.stack([t, t], dim=2)
print("t_test:{} shape:{}".format(t_test, t_test.shape))

#res
t_test:tensor([[[1., 1.],
         [1., 1.],
         [1., 1.]],

        [[1., 1.],
         [1., 1.],
         [1., 1.]]]) shape:torch.Size([2, 3, 2])

#在已有维度创建
t = torch.ones((2, 3))
t_test = torch.stack([t, t, t], dim=0)
print("t_test:{} shape:{}".format(t_test, t_test.shape))

#res
t_test:tensor([[[1., 1., 1.],
         [1., 1., 1.]],

        [[1., 1., 1.],
         [1., 1., 1.]],

        [[1., 1., 1.],
         [1., 1., 1.]]]) shape:torch.Size([3, 2, 3])

!cat不会扩充张量维度，但是stack会扩充张量维度
3.torch.chunk()
功能:将张量按维度dim进行平均切分
返回值:张量列表
若不能整除，最后一份张量小于其他张量

torch.chunk(input, #要切分的张量
	chunks, #要切分的份数
	dim=0  #要切分的维度
)

#实例
a = torch.ones((2, 5))  
list_of_tensors = torch.chunk(a, dim=1, chunks=2) 
for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}，shape is{}".format(idx + 1, t, t.shape))

#res
第1个张量：tensor([[1., 1., 1.],
        [1., 1., 1.]])，shape istorch.Size([2, 3])
第2个张量：tensor([[1., 1.],
        [1., 1.]])，shape istorch.Size([2, 2])

4.torch.split()
功能:将张量按维度dim进行切分
返回值:张量列表

torch.split(tensor, #要切分的张量
	split_size_or_sections, #为int时，表示每一份的长度；为list时，按list元素切分
	dim=0
)

# int实例
t = torch.ones((2, 5))
list_of_tensors = torch.split(t, 2, dim=1)  # [2 , 1, 2]
for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx + 1, t, t.shape))
# res
第1个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
第2个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
第3个张量：tensor([[1.],
        [1.]]), shape is torch.Size([2, 1])

#list实例
t = torch.ones((2, 5))
list_of_tensors = torch.split(t, [2, 1, 2], dim=1)  # [2 , 1, 2]
for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx + 1, t, t.shape))
#res
第1个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
第2个张量：tensor([[1.],
        [1.]]), shape is torch.Size([2, 1])
第3个张量：tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
!注意:list切分时，list里数据求和后等于dim对应的长度

2.张量索引

1.torch.index_select()
功能：在维度dim上，按index索引数据
返回值：依index索引数据拼接的张量

torch.index select(input, #要索引的张量
	dim, #要索引的维度
	index, #要索引数据的序号 #dtype不能是float，选用整形
	out=None
)
#实例
t = torch.randint(0, 9, size=(3, 3))
idx = torch.tensor([0, 2], dtype=torch.long)  
t_select = torch.index_select(t, dim=0, index=idx)
print("t:\n{}\nt_select:\n{}".format(t, t_select))

#res
t:
tensor([[4, 5, 0],
        [5, 7, 1],
        [2, 5, 8]])
t_select:
tensor([[4, 5, 0],
        [2, 5, 8]])

2.torch.masked_select()
功能：按mask中的True进行索引
返回值：一维张量

torch.masked_select(input, #要索引的张量
	mask, #与input同形状的布尔类型张量
	out=None
)
#example
t = torch.randint(0, 9, size=(3, 3))
mask = t.le(5)  # ge is mean greater than or equal(>=)/   gt: greater than(>)  le(<=)  lt(<)
t_select = torch.masked_select(t, mask)
print("t:\n{}\nmask:\n{}\nt_select:\n{} ".format(t, mask, t_select))

#res
t:
tensor([[4, 5, 0],
        [5, 7, 1],
        [2, 5, 8]])
mask:
tensor([[ True,  True,  True],
        [ True, False,  True],
        [ True,  True, False]])
t_select:
tensor([4, 5, 0, 5, 1, 2, 5])

3.张量变换

1.torch. reshape( )
功能：变换张量形状
注意事项：当张量在内存中是连续时，新张量与input共享数据内存

torch.reshape(input, #要变换的张量
	shape  #新张量的形状
)


#example
t = torch.randperm(8)
t_reshape = torch.reshape(t, (-1, 2, 2))  # -1代表该维度不需要关心，根据其他维度计算而来
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))

t[0] = 1024
print("t:{}\nt_reshape:\n{}".format(t, t_reshape))
print("t.data 内存地址:{}".format(id(t.data)))
print("t_reshape.data 内存地址:{}".format(id(t_reshape.data)))

#res
t:tensor([5, 4, 2, 6, 7, 3, 1, 0])
t_reshape:
tensor([[[5, 4],
         [2, 6]],

        [[7, 3],
         [1, 0]]])
t:tensor([1024,    4,    2,    6,    7,    3,    1,    0])
t_reshape:
tensor([[[1024,    4],
         [   2,    6]],

        [[   7,    3],
         [   1,    0]]])
t.data 内存地址:1921793389440
t_reshape.data 内存地址:1921722186048
#示例视频里内存一样，不知道此处为何不相等

2.torch.transpose()
功能交换张量的两个维度
3.torch.t()
功能：2维张量转置，对矩阵而言，等价于
torch.transpose(input,0,1)

torch.transpose(input,#要变换的张量
	dim0, #要交换的维度
	dim1 #要交换的维度
)
#example
# torch.transpose
t = torch.rand((2, 3, 4))
t_transpose = torch.transpose(t, dim0=1, dim1=2)  # c*h*w     h*w*c
print("t shape:{}\nt_transpose shape: {}".format(t.shape, t_transpose.shape))

#res
t shape:torch.Size([2, 3, 4])
t_transpose shape: torch.Size([2, 4, 3])


torch.t(input)

4.torch.squeeze()
功能：压缩长度为1的维度(轴)

torch.squeeze(input,
	dim=None,#若为None,移除所有长度为1的轴;若指定维度,当且仅当该轴长度为1时,可以被移除
	out=None
)

#example
t = torch.rand((1, 2, 3, 1))
t_sq = torch.squeeze(t)
t_0 = torch.squeeze(t, dim=0) #长度为1移除
t_1 = torch.squeeze(t, dim=1) #长度为2不移除
print(t.shape)
print(t_sq.shape)
print(t_0.shape)
print(t_1.shape)

#res
torch.Size([1, 2, 3, 1])
torch.Size([2, 3])
torch.Size([2, 3, 1])
torch.Size([1, 2, 3, 1])

3.5 torch.unsqueeze()
功能：依据dim扩展维度

torch.usqueeze(input,
	dim, #扩展的维度
	out=None
)

4.张量数学运算

torch.add()
torch.addcdiv()
torch.addcmul()
torch.sub()
torch.div()
torch.mul()

torch.log(input,out=None)
torch.log10(input,out=None)
torch.log2(input,out=None)
torch.exp(input,out=None)
torch.pow()

torch.abs(input,out=None)
torch.acos(input,out=None)
torch.cosh(input,out=None)
torch.cos(input,out=None)
torch.asin(input,out=None)
torch.atan(input,out=None)
torch.atan2(input,other,out=None)

torch.add()
功能：逐元素计算 input+alpha×other

torch.add(input, #第一个张量
	alpha=1, #乘项因子
	other,  #第二个张量
	out=None
)

#example
t_0 = torch.randn((3, 3))
t_1 = torch.ones_like(t_0)
t_add = torch.add(t_0, 10, t_1)

print("t_0:\n{}\nt_1:\n{}\nt_add_10:\n{}".format(t_0, t_1, t_add))

#res
t_0:
tensor([[ 0.6614,  0.2669,  0.0617],
        [ 0.6213, -0.4519, -0.1661],
        [-1.5228,  0.3817, -1.0276]])
t_1:
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])
t_add_10:
tensor([[10.6614, 10.2669, 10.0617],
        [10.6213,  9.5481,  9.8339],
        [ 8.4772, 10.3817,  8.9724]])

补

5.线性回归

1.线性回归是分析一个变量与另外一(多)个变量之间关系的方法
因变量：y
自变量：x
关系：线性
y = wx+b
分析：求解w,b

2.求解步骤
a.确定模型
Model: y = wx+b

b.选择损失函数
MSE:

c.求解梯度并更新w,b
w = w – LR * w.grad
b = b – LR * w.grad

3.线性回归模型的实现

# -*- coding:utf-8 -*-
"""
@file name  : lesson-03-Linear-Regression.py
@author     : tingsongyu
@date       : 2018-10-15
@brief      : 一元线性回归模型
"""
import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)

lr = 0.05  # 学习率    20191015修改

# 创建训练数据
x = torch.rand(20, 1) * 10  # x data (tensor), shape=(20, 1)
y = 2*x + (5 + torch.randn(20, 1))  # y data (tensor), shape=(20, 1)

# 构建线性回归参数
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)

for iteration in range(1000):

    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)

    # 计算 MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 反向传播
    loss.backward()

    # 更新参数
    b.data.sub_(lr * b.grad)
    w.data.sub_(lr * w.grad)

    # 清零张量的梯度   20191015增加
    w.grad.zero_()
    b.grad.zero_()

    # 绘图
    if iteration % 20 == 0:

        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
        plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
        plt.pause(0.5)

        if loss.data.numpy() < 1:
            break

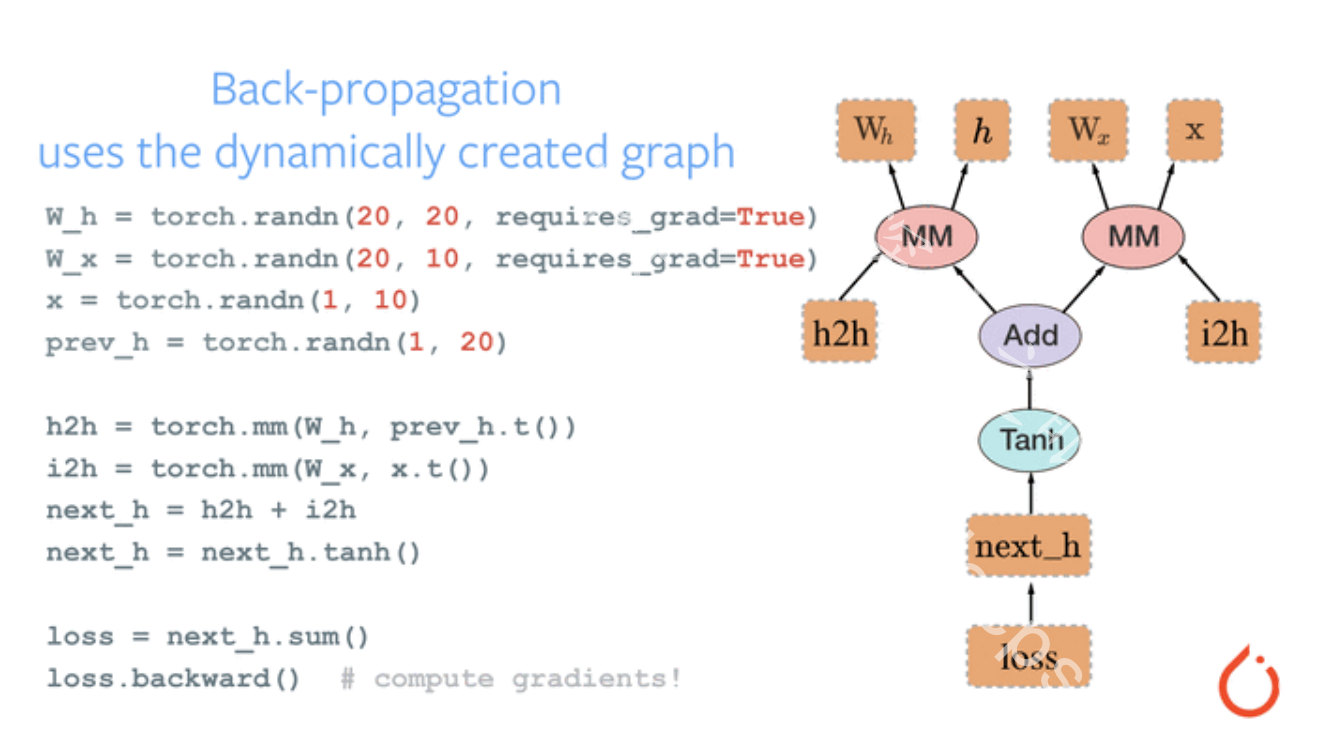
3.计算图与动态图机制

1.计算图

1.计算图是用来描述运算的有向无环图
计算图有两个主要元素：结点(Node)和边(Edge)

结点表示数据，如向量，矩阵，张量
边表示运算，如加减乘除卷积等

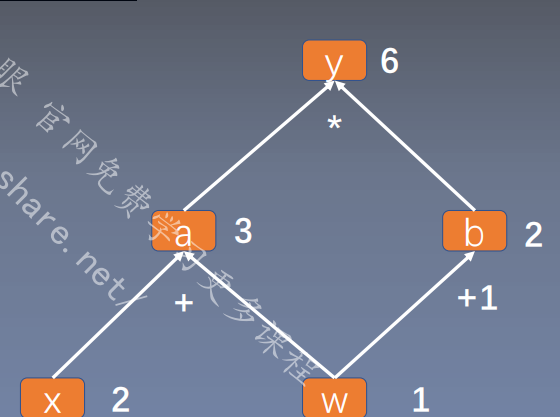
用计算图表示：y = (x+ w) * (w+1)
a = x + w
b = w + 1
y = a * b

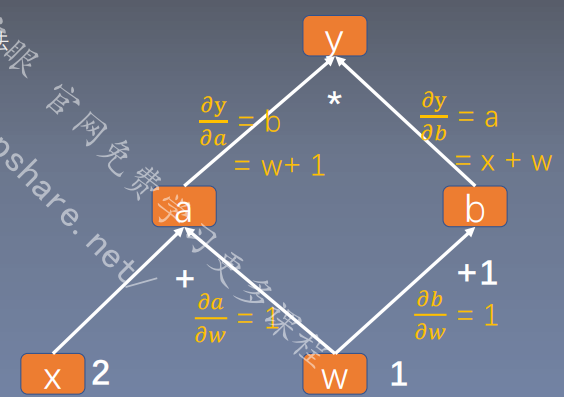
2.计算图与梯度求导
y = (x+ w) * (w+1)
y对w求偏导
y =2w + x + 1

# -*- coding:utf-8 -*-
"""
@file name  : lesson-04-Computational-Graph.py
@author     : tingsongyu
@date       : 2018-08-28
@brief      : 计算图示例
"""
import torch

w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)

a = torch.add(w, x)  # retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)
#查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)

#反向传播(求导)
y.backward()
print(w.grad)

#查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)

#查看 grad_fn
print("grad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)

#res
tensor([5.])
is_leaf:
 True True False False False
gradient:
 tensor([5.]) tensor([2.]) None None None
grad_fn:
 None None <AddBackward0 object at 0x00000190721A40D0> <AddBackward0 object at 0x00000190721DAD30> <MulBackward0 object at 0x0000019073FD35B0>

3.叶子结点：用户创建的结点称为叶子结点，如X与W
is_leaf: 指示张量是否为叶子结点
非叶子节点反向传播之后都会释放以节省内存开销
如果在反向传播之前执行retain_grad()方法，即可查看非叶子节点梯度

#例如
a = torch.add(w,x)
a.retain_grad()

4.grad_fn记录创建该张量时所用的方法
叶子节点的grad_fn为None
a,b通过加法得到所以grad_fn为<AddBackward0>
y通过乘法得到所以grad_fn为<MulBackward0>

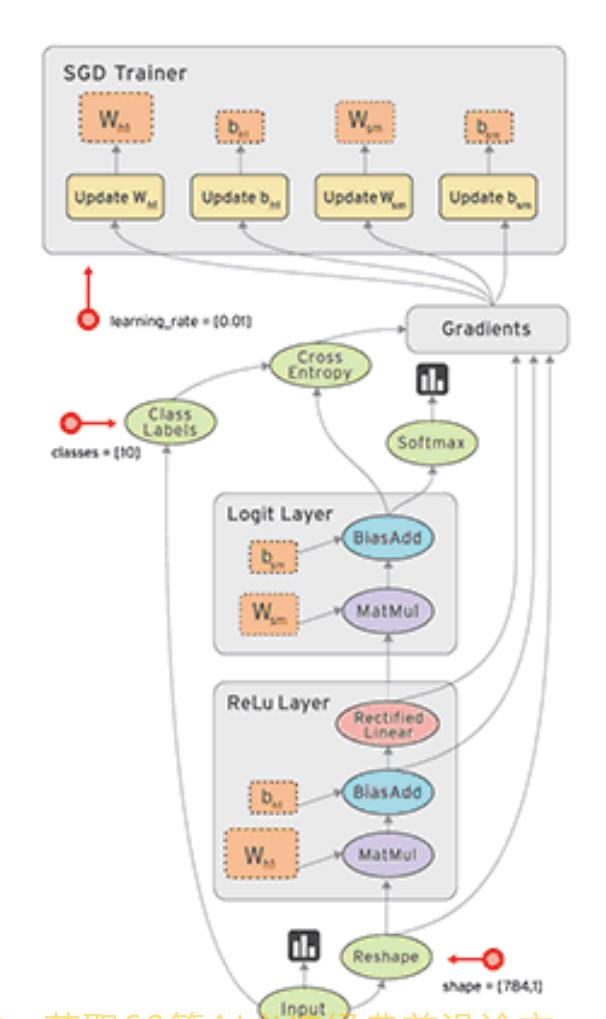
2.动态图

根据计算图搭建方式，可将计算图分为动态图和静态图
动态图:运算与搭建同时进行 灵活易调节
箭头理解成依赖于

静态图:先搭建图，后运算 高效不灵活

4.autograd与逻辑回归

1.autograd

1.backward

1.torch.autograd.backward
功能:自动求取梯度
• tensors: 用于求导的张量，如 loss
• retain_graph : 保存计算图
• create_graph : 创建导数计算图，用于高阶求导
• grad_tensors：多梯度权重

torch.autograd.backward(tensors,
	grad_tensors=None,
	retain_graph=None,
	create_graph=False
)

2.调用.backward方法就是调用torch.autograd.backward(调试可见)

要两次反向传播第一次需要保存计算图

w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)


y.backward(retain_graph=True)
# print(w.grad)
y.backward()

3.gradient设置多梯度权重
gradient 传入 torch.autograd.backward()中的grad_tensors

w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)

a = torch.add(w, x)  # retain_grad()
b = torch.add(w, 1)

y0 = torch.mul(a, b)  # y0 = (x+w) * (w+1)    dy0/dw = 5
y1 = torch.add(a, b)  # y1 = (x+w) + (w+1)    dy1/dw = 2

loss = torch.cat([y0, y1], dim=0)  # [y0, y1]
grad_tensors = torch.tensor([1.0, 2.0]) # 5 + 2*2

loss.backward(
    gradient=grad_tensors
)  # gradient 传入 torch.autograd.backward()中的grad_tensors

print(w.grad)
#tensor([9.])

2.grad

1.torch.autograd.grad
功能：求取梯度

torch.autograd.grad(outputs, #用于求导的张量，如loss
	inputs,                  #需要梯度的张量
	grad_outputs=None,       #多梯度权重
	retain_graph=None,       #保存计算图
	create_graph=False       #创建导数计算图，用于高阶求导
)

#example
x = torch.tensor([3.0], requires_grad=True)
y = torch.pow(x, 2)  # y = x**2
#一阶导
grad_1 = torch.autograd.grad(
    y, x, create_graph=True
)  # grad_1 = dy/dx = 2x = 2 * 3 = 6
print(grad_1)
#二阶导
grad_2 = torch.autograd.grad(grad_1[0], x)  # grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
print(grad_2)

#res 
(tensor([6.], grad_fn=<MulBackward0>),)
(tensor([2.]),)

2.注意:
a.梯度不自动清零

#example
w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)

for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b) 

    y.backward()
    print(w.grad)
#res
tensor([5.])
tensor([10.])
tensor([15.])
tensor([20.])

解出梯度后需要手动清零

w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)

for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b) 

    y.backward()
    print(w.grad)
    w.grad.zero_() #下划线是原地操作

#res 
tensor([5.])
tensor([5.])
tensor([5.])
tensor([5.])

b.依赖于叶子结点的结点，requires_grad默认为True

w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

print(a.requires_grad, b.requires_grad, y.requires_grad)

#res 
True True True

c.叶子节点不可执行in-place(原地操作)
反向传播过程中在求偏导时会得到包含叶子节点的项
例如 dy/da = b = w + 1最后会根据w所代表的内存地址取得w实际的数据，如果叶子节点执行in-place操作会导致数据出错。

w = torch.tensor([1.0], requires_grad=True)
x = torch.tensor([2.0], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
w.add_(1)
y.backward()

#res 
Traceback (most recent call last):
  File "main.py", line 127, in <module>
    w.add_(1)
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.

in-place操作学习

a = torch.ones((1,))
print(id(a), a)

#非原地操作
#a = a + torch.ones((1, )) 
#print(id(a), a)
#原地操作
a += torch.ones((1,))
print(id(a), a)

#res
2006144672256 tensor([1.])
2006144672256 tensor([2.])

原地操作要求前后操作变量内存地址不变
非原地操作会导致内存地址改变

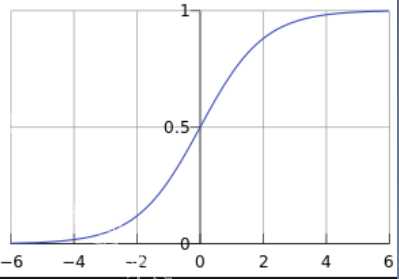
2.逻辑回归

1.逻辑回归是线性二分类模型

Sigmoid函数

对数几率回归等价于逻辑回归

2.线性回归与逻辑回归
线性回归是分析自变量x与因变量y(标量)之间关系的方法
逻辑回归是分析自变量x与因变量y(概率)之间关系的方法
3.实现
迭代训练步骤:
数据+模型+损失函数+优化器 ->迭代训练

# -*- coding: utf-8 -*-
"""
# @file name  : lesson-05-Logsitic-Regression.py
# @author     : tingsongyu
# @date       : 2019-09-03 10:08:00
# @brief      : 逻辑回归模型训练
"""
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)


#step 1/5 生成数据 
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias      # 类别0 数据 shape=(100, 2)
y0 = torch.zeros(sample_nums)                         # 类别0 标签 shape=(100, 1)
x1 = torch.normal(-mean_value * n_data, 1) + bias     # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums)                          # 类别1 标签 shape=(100, 1)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)


#step 2/5 选择模型
class LR(nn.Module):
    def __init__(self):
        super(LR, self).__init__()
        self.features = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.features(x)
        x = self.sigmoid(x)
        return x


lr_net = LR()   # 实例化逻辑回归模型


#step 3/5 选择损失函数
loss_fn = nn.BCELoss()

#step 4/5 选择优化器
lr = 0.01  # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)

#step 5/5 模型训练
for iteration in range(1000):

    # 前向传播
    y_pred = lr_net(train_x)

    # 计算 loss
    loss = loss_fn(y_pred.squeeze(), train_y)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()

    # 清空梯度
    optimizer.zero_grad()

    # 绘图
    if iteration % 20 == 0:

        mask = y_pred.ge(0.5).float().squeeze()  #以0.5为阈值进行分类
        correct = (mask == train_y).sum()  # 计算正确预测的样本个数
        acc = correct.item() / train_y.size(0)  # 计算分类准确率

        plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
        plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')

        w0, w1 = lr_net.features.weight[0]
        w0, w1 = float(w0.item()), float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6, 6, 0.1)
        plot_y = (-w0 * plot_x - plot_b) / w1

        plt.xlim(-5, 7)
        plt.ylim(-7, 7)
        plt.plot(plot_x, plot_y)

        plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
        plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
        plt.legend()

        plt.show()
        plt.pause(0.5)

        if acc > 0.99:
            break

2.Pytorch数据处理

3.Pytorch模型搭建

4.Pytorch损失优化

5.Pytorch训练过程

6.Pytorch的正则化

7.Pytorch的训练技巧

8.Pytorch深度体验